Relativističko sabiranje brzina

Relativističko sabiranje brzina 06.10.2012. u 12:17 · pre 171 mesec #1

Re: Relativističko sabiranje brzina 06.10.2012. u 21:27 · pre 171 mesec #2

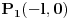
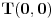
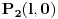
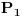
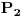
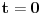
Dakle, imamo sistem S sa tačkama $P_1(-l,0)$ , $T(0,0)$ i $P_2(l,0)$ koje su nepokretne u njemu i posmatrače $P_1$ i $P_2$ koji se u trentku trenutku $t=0$ sistema S nalaze u istoimenim tačkama. Oba posmatrača jure ka tački $T$ brzinom $v\in(0,c)$ .

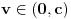
U sistemu S će se svakako sresti u tački $0$ u trenutku $l/v$ .

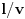
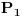
Razmotrimo sistem S' posmatrača $P_1$ sinhronizovan sa S. Zakoni transformacije su

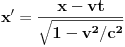
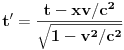
$x'=\frac{x-vt}{\sqrt{1-v^2/c^2}}$ , $t'=\frac{t-xv/c^2}{\sqrt{1-v^2/c^2}}$ .

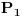
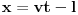
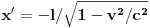
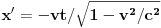
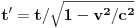
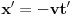
Obzirom da zakon kretanja posmatrača $P_1$ u sistemu $S$ glasi $x=vt-l$ , u sistemu S' se to svodi na $x'=-l/\sqrt{1-v^2/c^2}$ . Jednačina kretanja tačke $T$ u sistemu S glasi $x=0$ , što se u sistemu S' svodi na $x'=-vt/\sqrt{1-v^2/c^2}$ , $t'=t/\sqrt{1-v^2/c^2}$ , što zajedno daje zakon kretanja $x'=-vt'$ . Što se mesta i trenutka susreta sa tačkom $T$ tiče, treba rešiti sistem

$x'=-l/\sqrt{1-v^2/c^2}$ , $x'=-vt'$ .

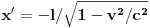
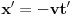
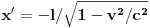
Dakle, mesto je $x'=-l/\sqrt{1-v^2/c^2}$ , a vreme $t'=(l/v)/\sqrt{1-v^2/c^2}$ .

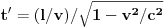
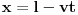
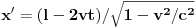
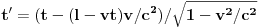
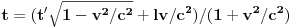
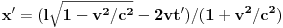
Da li je to mesto na kome će se u tom trenutku naći drugi posmatrač? Da vidimo: U sistemu S njegov zakon kretanja je $x=l-vt$ , što u sistemu S' daje $x'=(l-2vt)/\sqrt{1-v^2/c^2}$ , $t'=(t-(l-vt)v/c^2)/\sqrt{1-v^2/c^2}$ . Na osnovu druge jednačine je $t=(t'\sqrt{1-v^2/c^2}+lv/c^2)/(1+v^2/c^2)$ , pa kada to zamenimo u prvoj dobijamo da je $x'=(l\sqrt{1-v^2/c^2}-2vt')/(1+v^2/c^2)$ . 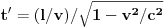Za $t'=(l/v)/\sqrt{1-v^2/c^2}$ dobija se tačno $x'=-l/\sqrt{1-v^2/c^2}$ .

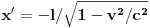
Dakle, opet se sve tri tačke susreću u istom trenutku.

Šta nije u redu?

Potpis

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Re: Relativističko sabiranje brzina 07.10.2012. u 13:08 · pre 171 mesec #3

Relativističko "sabiranje brzina" nije nikakvo sabiranje, već slaganje brzina ili još preciznije transformisanje jedne brzine iz jednog sistema u sistemu koji se u odnosu na njega kreće nekom drugom brzinom i ono znači da se u sistemu prvog posmatrača drugi njemu približava brzinom $2v/(1+v^2/c^2)$ . Stvarno, u sistemu S' je jednačina kretanja prvog posmatrača $x'=-l/\sqrt{1-v^2/c^2}$ , tj. on miruje u sistemu S', dok je jednačina kretanja drugog posmatrača u sistemu S' $x'=(l\sqrt{1-v^2/c^2}-2vt')/(1+v^2/c^2)$ , odnosno kreće se brzinom $2v/(1+v^2/c^2)$ .

Uopšte nije sporno da se u sistemu S rastojanje između posmatrača smanjuje brzinom $2v$ .

Potpis

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Re: Relativističko sabiranje brzina 07.10.2012. u 20:33 · pre 171 mesec #4

Citat:

Nedeljko: Uopšte nije sporno da se u sistemu S rastojanje između posmatrača smanjuje brzinom $2v$ .

Ali na krajevima tog odstojanja su promatrači pa bi za konkretnu vrednost brzine v
relativna brzina između njih bila 2v što je veće od c.

Re: Relativističko sabiranje brzina 07.10.2012. u 21:09 · pre 171 mesec #5

Potpuno je nevažno šta su te pokretne tačke. U sistemu S njihovo rastojanje se smanjuje vrzinom 2v. Da, ona je u tvom primeru veća od c. Pa?

Ja ne znam šta ti tačno podrazumevaš pod pojmom "relativna brzina". On se u STR obično odnosi na brzinu jedne tačke u sistemu u kome je druga tačka nepokretna. U ovom primeru to je sistem S' u kome se drugi posmatrač zaista kreće brzinom 2v/(1+(v/c)²)<c. No, pošto je pojam brzine relativan, tj. zavisi od izbora inercijalnog referentnog sistema, njeno izražavanje van konteksta ISR na koji se odnosi nema nikakvog smisla.

Po STR:

1. Ako neka tačka miruje u jednom IS, ona se u drugom IS kreće ravnomerno pravolinijski nekom brzinom v<c. Pritom je v isto za svaku tačku koja miruje u prvom IS.
2. Ako se neka tačka u jednom IS kreće brzinom manjom od c, onda se u svakom IS kreće brzinom manjom od c.
3. Ako se neka tačka u jednom IS kreće brzinom c, onda se u svakom IS kreće brzinom c.

Potpis

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Re: Relativističko sabiranje brzina 08.10.2012. u 08:34 · pre 171 mesec #6

Pod pojmom relativne brzine dvaju tela podrazumevam promenu odstojanja između njih.
Brzina promene odstojanja ne zavisi od referentnog sistema iz koga se promatra.
Brzina promene odstojanja, međutim, u str. je posledica Lorencovih transformacija i
definisana je izrazom v_r = (v₁ + v₂) /(1 + v₁v₂/c²)<c.
Ta brzina je promenljiva jer zavisi od proizvoda brzina v₁v₂.
Na osnovu tog izraza ne može se ustanoviti koja je stvarna relativna brzina između dva tela,
koja se kreću uniformnim brzinama, jer je za svaki referentni sistem drukčija.

Re: Relativističko sabiranje brzina 08.10.2012. u 14:43 · pre 171 mesec #7

Citat:

atelago: Brzina promene odstojanja ne zavisi od referentnog sistema iz koga se promatra.

Po STR zavisi.

Citat:

atelago: Brzina promene odstojanja, međutim, u str. je posledica Lorencovih transformacija i definisana je izrazom v_r = (v₁ + v₂) /(1 + v₁v₂/c²)<c.

Nije. Ako se u jednokm sistemu dve tačke kreću u istom pravcu, a suprotnim smerovima brzinama $v_1$ i $v_2$ , onda se u drugom sistemu u kome jedna od tih tačaka miruje druga kreće brzinom $\frac{v_1+v_2}{1+v_1v_2/c^2}<c$ . To je značenje tog obrasca, a ne to što si napisao.

Potpis

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Re: Relativističko sabiranje brzina 08.10.2012. u 18:52 · pre 171 mesec #8

Mogao bi prvo da naučiš neku teoriju pre nego što je kritikuješ. Isto kao sa realnim brojevima.

Potpis

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Re: Relativističko sabiranje brzina 09.10.2012. u 00:14 · pre 171 mesec #9

6p215z[1].jpg63.08k

Re: Relativističko sabiranje brzina 09.10.2012. u 15:48 · pre 171 mesec #10

Ne možeš tako napamet da pišeš brzine u drugom sistemu bez transformacije vrzina. Ako se u polaznom sistemu taj drugi sistem kreće prvom telu u susret brzinom $\Delta v$ , onda su brzine u tom drugom sistemu

$v_a=\frac{v_1+\Delta v}{1+v_1\Delta v/c^2}$ , $v_b=\frac{v_2-\Delta v}{1-v_2\Delta v/c^2}$ .

U sistemu u kome prvo telo miruje, drugo se kreće brzinom

$\frac{\frac{v_1+\Delta v}{1+v_1\Delta v/c^2}+\frac{v_2-\Delta v}{1-v_2\Delta v/c^2}}{1+\frac{v_1+\Delta v}{1+v_1\Delta v/c^2}\frac{v_2-\Delta v}{1-v_2\Delta v/c^2}/c^2}=\frac{v_1+v_2}{1+v_1v_2/c^2}$ .

Zamisli da je svaka brzina predstavljena kao tangens hiperbolički nekog parametra pomnožen sa c. Pri slaganju brzina se ne sabiraju brzine, već parametri.

$u=\tanh(x)c$ , $v=\tanh(y)c$ ,
$\frac{u+v}{1+\frac{uv}{c^2}}=\frac{\tanh(x)c+\tanh(y)c}{1+\frac{(\tanh(x)c)(\tanh(y)c)}{c^2}}=\frac{\tanh(x)+\tanh(y)}{1+\tanh(x)\tanh(y)}c=\tanh(x+y)c$ .

Potpis

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Re: Relativističko sabiranje brzina 12.10.2012. u 08:32 · pre 171 mesec #11

Citat:

atelago:
Brzina promene odstojanja ne zavisi od referentnog sistema iz koga se promatra.

Citat:

Nedeljko: Po STR zavisi.

Citat:

Nedeljko:
U sistemu u kome prvo telo miruje, drugo se kreće brzinom
$\frac{\frac{v_1+\Delta v}{1+v_1\Delta v/c^2}+\frac{v_2-\Delta v}{1-v_2\Delta v/c^2}}{1+\frac{v_1+\Delta v}{1+v_1\Delta v/c^2}\frac{v_2-\Delta v}{1-v_2\Delta v/c^2}/c^2}=\frac{v_1+v_2}{1+v_1v_2/c^2}$ .

Re: Relativističko sabiranje brzina 12.10.2012. u 12:02 · pre 171 mesec #12

Da, u polaznom sistemu se rastojanje smanjuje brzinom $v_1+v_2$ , a u sistemu u kome jedno od tih tela miruje, rastojanje se smanjuje brzinom $\frac{v_1+v_2}{1+v_1v_2/c^2}$ . Te dve vrednosti se razlikuju kad god je $v_1v_2\neq 0$ .

Na koliko god ispravnih načina da računaš brzinu jednog od ta dva tela u sistemu u koem drugo telo miruje, dobićeš isti rezultat.

Potpis

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Re: Relativističko sabiranje brzina 12.10.2012. u 12:06 · pre 171 mesec #13

Samo još da dodam šta je tangens hiperbolički.

$\tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$ .

Potpis

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Re: Relativističko sabiranje brzina 12.10.2012. u 21:30 · pre 171 mesec #14

Citat:

Nedeljko: Po STR zavisi.

Citat:

$\frac{\frac{v_1+\Delta v}{1+v_1\Delta v/c^2}+\frac{v_2-\Delta v}{1-v_2\Delta v/c^2}}{1+\frac{v_1+\Delta v}{1+v_1\Delta v/c^2}\frac{v_2-\Delta v}{1-v_2\Delta v/c^2}/c^2}=\frac{v_1+v_2}{1+v_1v_2/c^2}$ .

Ništa značajno. Samo sam hteo da pokažem da drugi citat dematuje prvi.
Ostalo je nepotrebno.

Re: Relativističko sabiranje brzina 12.10.2012. u 21:44 · pre 171 mesec #15

$v_1+v_2\neq\frac{v_1+v_2}{1+v_1v_2/c^2}$ ,
a ti nastavi da troluješ.

Potpis

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Re: Relativističko sabiranje brzina 13.10.2012. u 00:12 · pre 171 mesec #16

A ti nastavi da grešiš po običaju. Ovo što si napisao pokazuje tvoje nerazumevanje
moje primedbe - ja sam tvrdio da relativna brzina između dva tela ne zavisi od toga
iz kog se inercijalnog sistema posmatraju i to je istina bilo da ih posmatramo na
klasičan ili na relativistički način - klasični način je jasan sam po sebi, a relativistički
si upravo ti dokazao. Kad ti nađem grešku onda prelaziš na lični plan jer to ne umeš
ni da priznaš niti umeš da podneseš.

Citat:

Nedeljko: $v_1+v_2\neq\frac{v_1+v_2}{1+v_1v_2/c^2}$ ,
a ti nastavi da troluješ.

Mešanje jednog i drugog načina posmatranja nije ispravno i to priznajem jer ne može
jedna relativistička nebuloza pomešana sa ispravnim tumačenjem dati ispravan rezultat.

Sam si sračunao da je za suret triju tačaka potrebno vreme za konkretne podatke u
zadatku iznosilo nešto malo preko jedne sekunde za put između tog promatrača i
tačke susreta t. j. kada će promatrač P₁ doći na mesto susreta, ali si
zaboravio da su promatrači P₁ i P₂ pre susreta bili na rastojanju
dvaput većem od tog puta i da to rastojanje ne može da se smanji na nulu za to
vreme ako brzina smanjivanja rastojanja nije veća od c.
Za moje "trolovanje" ni u fizici ni u matematici nisi dao nikakav vredan odgovor koji
pobija moje tvrdnje ili pretpostavke.

Re: Relativističko sabiranje brzina 13.10.2012. u 01:44 · pre 171 mesec #17

U sistemu S u kome si formulisao problem, brzina približavanja je $v_1+v_2$ .

U sistemu S' u kome jedno telo miruje je brzina približavanja $\frac{v_1+v_2}{1+v_1v_2/c^2}$ .

Je li to isto? Nije!

Uzeo si neki treći sistem S'', pa tražio brzine u njemu, u kome je brzina približavanja nešto sasvim treće $\frac{v_1+\Delta v}{1+v_1\Delta v/c^2}+\frac{v_2-\Delta v}{1-v_2\Delta v/c^2}$ . No, kada se iz tog trećeg sistema vrati u drugi S', brzina približavanja je opet $\frac{v_1+v_2}{1+v_1v_2/c^2}$ .

Dokazao sam da dva načina računanja brzine približavanja u S' daju isti rezultat, kao što je i očekivano, a brzine udaljavanja u S, S' i S'' se očigledno razlikuju.

Potpis

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Re: Relativističko sabiranje brzina 13.10.2012. u 10:10 · pre 171 mesec #18

Citat:

Nedeljko:Je li to isto? Nije!

Naravno da nije isto. To nisam ni tvrdio jer jedno je tačno a drugo pogrešno.

Citat:

Uzeo si neki treći sistem S'', pa tražio brzine u njemu, u kome je brzina približavanja nešto sasvim treće ...

Nije treće. Umesto tvog principa svođenja na sistem u kom jedno telo miruje dovoljno je
sračunati vektorsku razliku brzina na klasičan način u bilo kom inercijalnom sistemu pa je
relativna brzina između tela jednaka ukoliko je u tim sistemima vektorska razlika brzina
jednaka.

Tu razliku ipak računate na klasičan način a ne _slaganjem brzina!

Ovaj princip jednako važi za oba načina sračunavanja relativnih brzina t. j. ne zavisi od
inercijalnih referentnih sistema iz kojih se to čini.

Citat:

Dokazao sam da dva načina računanja brzine približavanja u S' daju isti rezultat, ...

Da, ali nisi pokazao kako je promatrač P₁ mogao dobiti informaciju od P₂
koji je bio udaljen 599584 km.

Re: Relativističko sabiranje brzina 13.10.2012. u 11:31 · pre 171 mesec #19

U STR se relativna brzina između da tela A i B definiše kao brzina jednog od ta dva tela tela u sistemu u kome drugo od ta dva tela miruje. Ta brzina ne zavisi od toga da li smo izabrali sistem u kome telo A miruje ili sistem u kome btelo B miruje. Brzina tela B u sistemu u kome telo A miruje jednaka je brzini tela A u sistemu u kome telo B miruje.

E, sad, ti imaš drugačiju terminologiju. Misliš na brzinu promene rastojanja između tela A i B. Ta veličina itekako zavisi od izbora ISR. Ta veličina se u nekom ISR računa tako što odrediš zakone brzina tih tela u tom ISR, pa onda brzine klasično sabereš/oduzmeš.

Šta nije jasno?

Citat:

atelago: Da, ali nisi pokazao kako je promatrač P₁ mogao dobiti informaciju od P₂
koji je bio udaljen 599584 km.

Koju informaciju? Ovde se radi o našem postupku računanja koga oni ne moraju biti svesni.

Potpis

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

1

Re: Relativističko sabiranje brzina 15.10.2012. u 05:35 · pre 170 meseci #20

Citat:

Nedeljko: U STR se relativna brzina između da tela A i B definiše kao brzina jednog od ta dva tela tela u sistemu u kome drugo od ta dva tela miruje. Ta brzina ne zavisi od toga da li smo izabrali sistem u kome telo A miruje ili sistem u kome btelo B miruje. Brzina tela B u sistemu u kome telo A miruje jednaka je brzini tela A u sistemu u kome telo B miruje.

Nije! Te brzine su jednake po skalarnoj vrednosti, ali suprotne po smeru.
Drugo: Šta su brzine V₁ i V₂? Koje su vrednosti tih brzina i kako se određuju?
Treće: Pokazao si da Δv ne utiče na relativističko sračunavanje brzine između dva tela
ali ti nije jasno šta znači Δv?
Četvrto: Znaš da _slažeš brzine, ali si zaboravio kako se sabiraju.
Peto: Ne bi trebalo da ponavljaš greške na koje ti je već ukazano.

Citat:

Misliš na brzinu promene rastojanja između tela A i B.

Naravno, to je skalarna vrednost relativne brzine između dva tela.

Citat:

Šta nije jasno?

Tebi nije jasno značenje brzine Δv.

Citat:

Koju informaciju?

P₁ nije znao da je P₂ crnac.

Citat:

Ovde se radi o našem postupku računanja koga oni ne moraju biti svesni.

Kakve to veze ima? Pišeš svašta u pravom smislu te reči, a druge optužuješ da troluju.

Forum kao aplikacija na telefonu

Srodne teme