To što si napisao jeste tačno, ali... uvek ima neko ali. Pošto fizika nije počela, a nije se ni završila sa Ajnštajnom, naše shvatanje Lorencovih transformacija se malo izmenilo i cela priča danas dobija simetrijski prizvuk, kako i priliči modernom duhu teorijske fizike u čijim osnovama su ugrađeni simetrijski principi. Stoga, neću se držati istorije u izlaganju, pisaću sa tačke gledišta moderne fizike u nameri da presečem niz misaonih eksperimenata kojima ste se obilno služili na ovoj temi u nedostatku adekvatnog poznavanja fizike i matematike ili nedostatka želje da se ista i koristi.
Simetrijski rečeno, Lorencove transformacije su sve izometrije prostora Minkovskog. Ovo, doduše, nije baš tačno zato što Lorencove transformacije ne obuhvataju translacije. Pošto su translacije značajne zbog toga što su generisane impulsima, pogodnije i celishodnije je raditi sa Poenkareovom grupom (Lorencove + translacije), a potom se zaključci lako izvode i za Lorencovu grupu zato što ona čini invarijantnu podgrupu unutar Poenkareove grupe.
Ovo je bilo malo zbrda-zdola pa ću sada krenuti lagano ispočetka. Zato sledi jedan mali flešbek na nerelativističku fiziku.
Duboko u telu Njutn-Galilejeve fizike leži jedna osobina koja je fundamentalna za fiziku niskih energija ljudske svakodnevice, ali pre nego što dođemo do nje da se podsetimo malo. Opis ove fizike je smešten u dobro nam poznati trodimenzionalni Euklidov prostor. Položaj sistema je zadat vektorom, a uloga vremena je samo u parametrizaciji putanja po kojima se kreću čestice. Osnovna osobina svih zakona nerelativističke fizike je da su oni nepromenljivi pri transformacijama (primenjenim na fizički sistem, ili na koordinatni sistem, samo u suprotnom smeru - što odgovara aktivnoj i pasivnoj reprezentaciji) koje ne menjaju rastojanja. Tj. neki fizički proces koji se odigrava na određeni način se neće promeniti ako celokupan sistem zarotiramo ili ga transliramo, ili obrnuto, ako ga posmatramo iz koordinatnog sistema koji je zarotiran ili transliran. Ovo zapažanje je od fundamentalnog značaja, zato što ako promenimo logiku i zahtevamo da fizički zakoni za simetrije imaju izometrije Euklidovog prostora, kao rezultat ćemo dobiti zakone kretanja i zakone održanja, tj. zakoni simetrije leže ispod dinamičkih zakona i u neku ruku su fundamentalniji od njih.
Dakle, nerelativistička fizika: (relativni)Položaji su dati vektorom u trodimenzionalnom prostoru
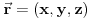
, a rastojanja su data sa
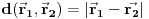
. Sve transformacije
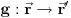
koje ne menjaju rastojanja čine algebarsku grupu i predstavljaju izometrije Euklidovog prostora. Osnovni dinamički zakoni moraju biti takvi da ih ove transformacije ne menjaju. Kada smo ovo shvatili, sama struktura prostora nam daje relevantne fizičke veličine i zakone održanja. Grupa o kojoj sam govorio se naziva Galilejeva grupa i razlaže se na prozvod sledećih podgrupa: translacije, rotacije, bustovi (transformacije između sistema koji se kreću konstantim brzinama, jedni u odnosu na druge) i inverzije (nisu naročito bitne za fiziku). Matematički gledano, ova grupa je Lijeva grupa. Svaka Lijeva grupa je kontinualno beskonačna, ali se ispostavlja da je određena konačnim skupom operatora koji se zovu generatori grupe. Pošto su matematički izrazi za transformacije poznati, jer je reč o običnoj geometriji, generatori se mogu naći i ispostavlja se sledeće: operatori koji generišu transformacije odgovaraju impulsu, generatori rotacija su momenti impulsa, dok generatori bustova nemaju naročit fizički značaj. Inverzije nemaju generatore zbog svoje diskretne strukture. Ovde vreme ne figuriše ravnopravno sa Euklidovim prostorom, ali ako bi se zasebno posmatralo vreme, kao osa, sama za sebe, mogli bismo da uvedemo i pojam vremenskih translacija, tj. reč je o prostom pomeranju početnog trenutka. Ovo je takođe simetrija zato što svi znamo još iz osnovne škole da početni trenutak možemo uvek izabrati onako kako nama odgovara. Ispostavlja se da vremenske translacije generiše operator energije. Postoji još jedna stvar bitna za vremenske translacije, a to je da one u stvari predstavljaju zakone kretanja, jer, ako razmislimo malo o tome šta znači translirati sistem iz nekog trenutka u neki budući trenutak vidimo da je u pitanju evolucija sistema iz jednog u drugi trenutak, onako kako mu je diktirano zakonima kretanja. Druga fundamentalna strana je u tome što automatski dobijamo zakone održanja: invarijantnost na neku transformaciju automatski povlači zakon održanja za veličinu koja je generiše. Tako da invarijantost na transformacije povlači zakon održanja impulsa, na rotacije, zakon održanja momenta impulsa i na vremenske translacije, zakon održanja energije. Ovime je zaokružena cela fizička slika samo na osnovu osobina prostora (dakle, proste geometrije - bez ikakvih hokus pokusa sa ogledalima, blizancima, časovnicima, liftovima, vozovima i ostalim gedankeneksperimentima, koje btw. smatram kontraproduktivnim, što skoro 80 strana ove teme pokazuje kao opravdano).
Eksperimentalno poznati nerelativistički mehanički zakoni se mogu reprodukovati ovim pristupom. Međutim problem postaju elektrodinamički zakoni zadati Meksvelovim jednačinama. Grupa simetrija elektrodinamike prosto i jednostavno NIJE Galilejeva grupa. Tj. ako primenimo transformacije iz Galilejeve grupe, nećemo dobiti identičnu sliku što je u koliziji sa osnovnim principom simetrija, tj. da osnovni dinamički zakoni moraju da dele simetrije sa prostorom. Sada možemo pretpostaviti sledeće: Meksvelove jednačine nisu ispravne (iako ih svi eksperimenti spektakularno potvrđuju), mehaničke jednačine nisu ispravne ili ako smo malo dalekovidi, da su i jedne i druge ispravne, ali da mehaničke jednačine nismo imali prilike da ispitamo u domenu energija u kome se normalno odvijaju elektromagnetni procesi te bi ih stoga možda trebalo malo uopštiti. Plan napada bi stoga bio sledeći: Pronaći simetriju Meksvelovih jednačina i potom naći mehaničke zakone koje ona reprodukuje i uporediti ih sa ranije poznatim zakonima. Ako u limesu niskih energija prelaze u nerelativističke zakone, uboli smo sedmicu.
Iz Meksvelovih jednačina je moguće matematičkim putem izvući njihove simetrije, ali to je previše mukotrpan posao, pogotovu što igrom slučaja rešenje leži na stolu. Dotičnom igrom slučaja Majkelson-Morlijev eksperiment je predložio kandidata: Iz ovog eksperimenta sledi da izgleda da je veličina zadata
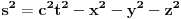
invarijantna pri rotacijama, vremenskim i prostornim translacijama, bustovima i inverzijama. Eto odmah ideje za simetrije: simetrije su sve operacije
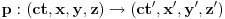
takve da vrednost prethodnog izraza ostavljaju nepromenjenim. Na osnovu ovoga odmah konstruišemo grupu simetrija i nalazimo formu njenih elemenata. Ova grupa simetrija se naziva Poenkareova grupa i isto kao Galilejeva grupa se razlaže ne proizvod podgrupa: translacija, rotacija, bustova i inverzija. Međutim, u pitanju je različiti entitet, zato što deluje na drugačiju geometrijsku strukturu koja je zadata četvorkom brojeva
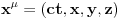
i metrikom
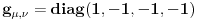
. Stoga će translacije obuhvatiti i prostorne i vremenske translacije što će imati neke zanimljive posledice koje ćemo objasniti odmah. Naime, kada nađemo generator translacija i malo bolje ga pogledamo, videćemo da on u sebe objedinjuje operatore energije i operatore impulsa što je i logična posledica ujedinjavanja vremenskih i prostornih translacija. Ovde je zgodno mesto da se izdvoji potklasa koordinatnih sistema koji imaju osobinu da se u njima prostorne komponente operatora impulsa anuliraju. Ove koordinatne sisteme ćemo nazvati sistemima mirovanja. Oni nam omogućuju da uvedemo parametar koji jednoznačno određuje svojstvene vrednosti operatora impulsa u sistemima mirovanja. Taj parametar ćemo nazvati masom. Kako je operator impulsa generator simetrija, za njega važi zakon održanja pa sledi da su njegove svojstvene vrednosti konstante evolucije pa predstavljaju zgodne parametre za račun te ih zato izdvajamo i stavljamo na pijedestal značajnih fizičkih veličina (eto vam simetrijske definicije mase). Rotacije će nam opet dati operatore momenta impulsa za generatore, koji će za uzvrat da nam daju njihove svojstvene vrednosti koje ćemo nazvati spinom. Pošto su momenti impulsa generatori simetrije, oni su održane veličine, te su njihove svojstvene vrednosti zgodni parametri pa i njih, tj. spin, stavljamo na pijedestal pored mase. Bustovi su zasebna priča, zato što nam njihovi generatori nisu od nekog naročitog fizičkog značaja. Međutim, pošto smo se mi uhvatili specijalnih koordinatnih sistema, sistema mirovanja, u kojima fizičke veličine i relacije među njima poprimaju posebno zgodan i jednostavan oblik, bustovi nam služe da zaključke izvedene u sistemima mirovanja prebacimo u bilo koji sistem u kome operator impulsa ima nenulte prostorne komponente. Kada malo pročačkamo bustove, među njima ćemo naći i one koji su građanstvu poznati kao Lorencove transformacije (tj. ono što ste vi navodili u prethodnim postovima). Oni naravno povlače za sobom sve one dilatacije vremena, dužine i ostale zanimacije za široke narodne mase i sve je to u osnovi posledica pretpostavke da transformacije koje ne menjaju izraz
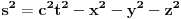
čine grupu simetrija fizičkih zakona.
OK, pretpostavka da je Poenkareova relevantna se držala samo na lepe oči. Izveli smo važne zaključke vezane za Poenkareovu grupu, sada moramo proveriti nekoliko stvari. Kao prvo, da li je Poenkareova grupa grupa simetrije Meksvelovih jednačina. Odgovor je naravno da. I ne samo to, ovo nam daje dodatni uvid u strukturu elektrodinamike. Naime, četiri Meksvelove jednačine se redukuju u dve i to kako. Ispostavlja se da je jedna od tih jednačina odgovorna za dinamiku, a da je druga čisto kinematička stvar, dakle nema nikakve veze sa fizikom već samo sa geometrijom, tj. ona predstavlja matematički identitet koji se naziva Bjankijev identitet. Dakle, dobili smo i jedno zanimljivo saznanje, a to je da se dve bezizvorne Meksvelove jednačine spajaju u jednu koja je čisto kinematička. Druge dve, sa izvorima, se spajaju u jednu koja je odgovorna za dinamiku. Znači, naša pretpostavka je ispunila prvi zahtev i više nego uspešno. Drugo je da proverimo kakve mehaničke zakone reprodukuje Poenkareova grupa. Ona će reprodukovati jednačine koje su poznate kao relativstičke jednačine kretanja. Ono što nas zanima je kakav je limes niskih energija. I tu je bingo. Jednačine se u limesu niskih energija redukuju u, stare dobre, 400 godina poznate, nerelativističke jednačine.
Dakle, ono što je poznato kao specijalna teorija relativnosti je direktna posledica simetrija u prostoru Minkovskog. Ukoliko specijalna teorija relativnosti, kao jedan veoma uzan deo, cele široke priče, ne bi bila tačna to bi značilo da simetrije u prostoru Minkovskog nisu simetrije sveta u kome živimo. Međutim, kao što sam već pomenuo specijalna teorija relativnosti je samo jedan mali deo koji proističe iz ove simetrijske priče. Ovi simetrijski principi su ugrađeni u sve teorije interakcija koje poznajemo. Kvantne teorije interakcija koje imamo, teorija elektroslabih interakcija i kvantna hromodinamika su
eksplicitno izvedene iz simetrijskih principa, koji pored onih o kojima smo pričali i koji se zovu globalni, uključuju i lokalne (gejdž) simetrije. Dakle, prvi princip iz koga su ove teorije izvedene je princip simetrije sa Poenkareovom grupom kao relevantnom grupom. To je čovečanstvu dalo
najtačniju teoriju i najveću prediktivnu moć koju je ikada imalo. Na primer, predviđanja u kvantnoj elektrodinamici su testirana do na
neverovatnih 18 decimala.
Svaki eksperiment u fizici visokih energija izveden u poslednjih 60-70 godina se poklopio sa predviđanjima standardnog modela, koji je ponavljam, ab initio izveden iz simetrijskih principa. Ovo tim principima daje neoborivu podršku i uspostavlja Poenkareovu grupu kao grupu simetrija prostor-vremena. Ono što je sadržano u specijalnoj teoriji relativnosti direktna je posledica.
Ovo ti, nadam se, daje fundamentalniji i savremeniji pogled na stvari, pošto se rasprava o temi koju si ti pokrenuo ne može adekvatno voditi sredstvima koja ste ti i ostali na forumu koristili. Ne nadam se tome da razumeš sve što sam napisao, zato što je to nešto što sam ja učio četiri godine tako da očekujem pitanja u vezi ovoga i u vezi tvojih razmišljanja na temu specijalne teorije relativnosti.