Nula je u matematici neutralni element za sabiranje, odnosno takav broj da za svaki broj x važi x+0=x. Sve ostalo nije nula. Ako nemaš neutralni element za sabiranje, onda ni pojam suprotnog elementa za sabiranje (-x) nema smisla. Ukoliko ga imaš, on je jedinstven.
Nula je u matematici samo ono što ti zoveš apsolunom nulom i obeležavaš sa |0| i njome se ne može deliti. Ono šti ti zoveš nulom se zove beskonačno mala veličina ili infinitezimala. Infinitezimala nije nula. Upravo iz tog razloga, njome se može deliti. Neka zasnivanja analize isključuju infinitezimale (klasična analiza), a neke ih uključuju (nestandardna analiza). Uređeno polje bez infinitezimala se zove arhimedovsko, a bez infinitezimala nearhimedovsko polje. Polje realnih brojeva je maksimalno arhimedovsko polje, odnosno arhimedovsko polje (dakle, koje nema infinitezimale) takvo da svako proširenje tog polja do nekog uređenog polja uključuje infionitezimale. Dakle, u polju realnih brojeva infinitezimala nema.
Sa druge strane, u nestandardnoj analizi se radi nad jednim nearhimedovskim poljem, gde infinitezimala ima. U nearhimedovskom polju koje je dovoljno dobro za izlaganje analize se ne mogu sve pozitivne infinitezimale izraziti kao stepeni (sa realnim izložiocem) jedne infinitezimale. Skup infinitezimala mora biti mnogo bogatiji. Pošto se ne može istaći jedna infinitezimala preko koje bi se izražavale sve ostale, ne postoji univerzalna oznaka za jednu istaknutu infinitezimalu, već su sve ravnopravne.
I drugo, ne možeš uvesti infinitezimale, a ne uvesti elemente koji su beskonačno bliski broju 5. Kod tebe, kao da se može reći da je 5+0=5, a da ne može 0+0=0. I u infintezimalnom računu postoji jedna jedina nula. Infinitezimale su drugo.
U svakom slučaju, mora se znati sa čim se radi, i ne smeju se brkati babe i žabe. U klasičnoj analizi oznaka za limes služi da bi se razlikovao granični proces od njegovog rezultata, dok se u infinitezimalnom računu u tu svrhu koriste monade (skupovi svih međusobno beskonačno bliskih elemenata). Elementi nearhimedovskih polja odgovaraju graničnim procesima u klasičnoj analizi, a monade njihovim rezultatima. Svaki element pripada tačno jednoj monadi. Nemoj da misliš da se time ljudi nisu bavili.
Citat:
galet@world: Kaže se na primer da je jedan kroz beskonačno jednako nula.
U klasičnoj analizi se ponekad radi i sa proširenim skupom realnih brojeva, koji ne čini polje. Postoji teorema o algebarskim kombinacijama limesa po kojoj ako je
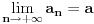
i
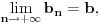
onda je i
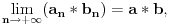
gde je

bilo koja od četiri računske radnje, uz ograničenje da ako se radi o delenju, pretpostavlja se da je
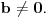
Tu su

i

realni, dakle konačni, brojevi.
To nam omogućava da izračunavamo neke limese. Postavlja se pitanje kako definisati operacije na proširenom skupu realnih brojeva tako da važi teorema o algebarskim kombinacijama limesa. Ako je niz

konvergentan ka nekom konažnom broju
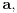
a niz
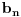
teži beskonačnosti, onda niz

teži nuli. Zbog toga se količnik realnog broja i beskonačnosti definiše kao nula. Podvlačim da u matematici postoji jedna jedina, što bi ti rekao "čista nula". Ovde ne govorim o infinitezimalama (koje nisu nule), već o klasičnoj analizi, koja isključuje infinitezimale. To nam onda omogućava da izračunavamo limese kao što je
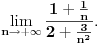
Tako da je

isto što i
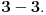
Citat:
galet@world: Dalje – ni po kojoj teoriji neki broj niti je veći niti manji od samog sebe. Ako podeliš taj broj sam sa sobom dobićeš rezultat 1.
Ovo nije tačno. Delenje nulom, na primer u matematičkoj analizi, je nedefinisano, osim ako nju ne smatraš teorijom. Naravno da nula nije ni veća ni manja od sebe, ali to ne znači da je možeš deliti samom sobom. Razmotri to na onoj svojoj "apsolutnoj nuli".
Citat:
galet@world: U tome se sastoji moja pobuna protiv nedefinisanosti funkcije 6x/3x za x = 0. Ali to je samo moja pobuna, a odatle može da se razvije nov pristup računanju sa nulom i beskonačno a i ne mora ako moja pobuna nema osnov. Ovo iznosim kao ideju koju neko može da u detalje razradi i definiše.
U matematici se za funkciju koja je nedefinisana u nekoj tački, a u celoj okolini te tačke, bez te tačke jeste, i ima limes u toj tački, kaže da u toj tački ima otklonjiv singularitet. Može se po konvenciji podrazumevati da su funkcije sa kojima se radi u svim takvim tačkama dodefinisane tako da u toj tački budu neprekidne. To je čest slučaj u kompleksnoj analizi. Međutim, to postiže posmatranjem ponašanja funkcije u okolini te tačke, a ne takvim dodefinisanjem osnovnih operacija. Premalo je informacija u toj tački, dok ih u okolini te tačke ima mnogo više. Stvar je u tome da operacija mora istim argumentima da dodeli uvek isti rezultat, inače nije operacija. U tvom slučaju nije jasno šta je to broj. Sa kakvim se objektima tu zapravo radi. Realni brojevi se na primer mogu precizno definisati preko beskonačnih decimalnih razvoja.
Citat:
galet@world: Ako na primer deliš ugao od jednog stepena na beskonačno dobićeš rezultat 00. Dakle ova nula ima dimenziju [0]. To je postojeći ugao i on može biti i pozitivan i negativan.
Opiši mi (geometrijski) to delenje, da vidimo taj ugao. Šta mu je teme, šta su mu kraci itd. Geometrijski, to i nije ugao. Može se eventualno smatrati uglom od nula stepeni, a nula nije ni pozitivna, ni negativna.
Ugao se svakako može podeliti na n delova za svaki prirodan broj n. U klasičnoj analizi su svi prirodni brojevi konačni, pa ova rasprava i nema mnogo smisla van konteksta koji sam već opisao. U nestandardnoj analizi prirodni brojevi mogu biti beskonačni, pa je takva podela u njoj potpuno legitimna. Međutim, u njoj dobijeni ugao nema nula stepeni, nego infinitezimalu stepeni. To nije isto.
Citat:
galet@world: Smatram da za nekog istraživača ovo može da bude vrlo interesantna tema.
Teško. Nearhimedovska polja su suviše rađena, i suviše se daleko otišlo u dubinu u njihovim istraživanjima, da bi teme ovog nivoa bile nekome zanimljive za proučavanje.
Citat:
galet@world: Odgovor je bio s vaše strane da kontakt može postojati samo u jednom inercijalnom sistemu, a u ostalim ne i t. d. (Srki). Ja se s tim nisam složio.
Nisi se složio, ali nisi ni izveo logičku kontradikciju unutar STR, koju si najavio. Fizika govori o tome šta će merni instrument da pokaže, dakle o onome što se može objektivno ustanoviti. Postojanje kontakta ne može. Probaj da zamisliš instrument kome će se upaliti sijalica ako i samo ako je došlo do premošćenja. Taj instrument "potopi" u univerzum u kome se premošćavanje odigrava, dakle u neki referentni sistem.
Citat:
galet@world: Postoji i logički put ako se tim putem nedvosmisleno može dokazati protivrečnost neke teorije u samoj sebi.
Ja sam napisao
Citat:
Nedeljko: Pod pretpostavkom da te teorije nisu protivrečne...
Dakle, isključio sam tu mogućnost. Naravno da je to jedan od načina da se obori teorija. No, STR ima matematički model, što je dokaz njene unutrašnje (ili logičke) neprotivrečnosti. Međutim, i kada se teorija obara na taj način, u tom izvođenju kontradikcije se mora strogo pridržavati postavki te teorije, opštih logičkih zakona i ničega više. Ukoliko u izvođenju koristiš neke druge postavke, onda ćeš eventualnim izvođenjem protivrečnosti oboriti njih.
Citat:
galet@world: Ja sam predložio eksperiment koji jednu od dve mogućnosti tumačenja konstantnosti brzine svetlosti (ili PSSS ili STR) isključuje.
Ja formulaciju tog eksperimenta nigde ovde nisam video.
Citat:
galet@world: Bilo bi još bolje kad bi ti imao malo više interesa na istraživačkom planu jer je to i najuzbudljiviji posao u ljudskoj delatnosti (opet po mom mišljenju!)
Da bi čovek nešto istraživao prvo mora da nauči ono što već postoji. Očigledno nisi temeljno prošao nijedan kurs matematičke analize. Tako se ne ide u istraživačke pohode.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.