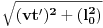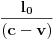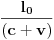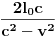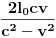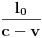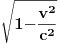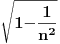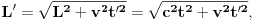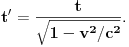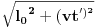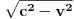Teorija Relativnosti

Fizička stvarnost omogućava nam da imamo u istom „događaju“: (0<v<c), c, v, (c+v), (c-v), (i sve između tog „maksimuma“ i „minimuma“, među kojima je i ), i to sve u zavisnosti gdje smjestimo „posmatrača“.Naš način računanja (ko i u odnosu na šta „vidi i računa“, mi ili naš „posmatrač“) neće imati nikakvog uticaja na tu fizičku stvarnost, ali ćemo imati matematičke relacije i rezultate u kojima je „sve moguće“ (c+v)/c i (c-v)/c.Diferencijalni račun u tom slučaju (u svijim „temeljima“ ima „ugrađen“ pravougli trougao) prevodi te matematičke iskaze uspostavljene u jednim fizičkim uslovima na druge fizičke uslove, prostimim stavom: Δt (ili neka druga veličina, sve jedno) teži... Takve slučajeve odlično obrađuju na mašinskim fakultetima: „nosač“, „relativna kretanja“, „relativne brzine“, „relativne sile“..., (u zavisnosti šta i u odnosu na šta mjere i računaju, gdje su „oslonci“, „vektorske baze“, „tenzora“,..). Zato su mogući i za naše posmatrače različiti sučajevi iskazivanja matematičkih istina, koje se u fizičkoj stvarnosti obistinjuju, računanjem predvide, pa eksperimentom potvrde. Zato je i moguće u matematičkom iskazu na jednoj strani jednakosti imati i veličine kojih „nema u fizičkoj stvarnosti nekog od posmatrača“, ili su drugačije (mase, sile, brzine, vremena,....).
Kako sve te različite slučajeve „mjerimo“ istom veličinom c, svi ti različiti slučajevi mogu da se obistine (predvide i eksperimentalno provjere i utvrde). I to baš svi slučajevi, bez iznimke.
U Ajnštajnovim i Lorencovim matematičkim relacijama imamo međuzavisne veličine (fizičke događaje) i iz te matematičke međuzavisnosti (u konkretnom fizičkom sadržaju) uočavam opštu zakonitost i na nju ukazujem. Ta opšta zakonitost se obistinjuje u fizičkoj stvarnosti, ali ne zbog „dilatacije vremena“ ili „kontrakcije dužina“.
Cibernoid, nacrtaj nam onu sliku (K₀K' = 2vt') „okomitog kretanja“ svjetlosti, sa okomitom dužinom PO = l₀ na sredini te dužine, pa da vidimo hoćeš li ti (iz K') mjeriti nešto drugo, a ja (iz K₀) nešto drugo.

Nedeljko (poruka 11. 12. u 11 i.): "Opisivanje relativističkog slaganja brzina matematičkom operacijom sabiranja je isto toliko pogrešno koliko i opisivanje relativističkog slaganja brzina operacijom množenja".
Ranije (tamo davno) tvrdio si da je u matematici sve moguće, ako se time može opisati i predvidjeti fizička stvarnost („eksperimentalno provjeriti“, dakle – obistiniti), a ja tvrdio da ima dosta sadržaja u matematici i dosta sadržaja u fizičkoj stvarnosti koje nisu u „zajedničkom presjeku“ (ali se mogu „preslikati“ u zajednički presjek). Primjeri: masa∙masa – ne postoji u fizičkoj stvarnosti, A'A = (2c)∙t (sam si naveo primjer za ovu matematičku istinu, a koja nije moguća u fizičkoj stvarnosti, a zar ovo nije baš pravi primjer „relativističkog slaganja brzina“ istog pravca – različitog smjera?), t∙t – ne postoji u fizičkoj stvarnosti, itd.
Ako ja („množenjem“) dobijem isti rezultat kao i ti ( i taj isti rezultat „eksperimentalno potvrđujemo“) zašto meni ne priznavati pravo na množenje (primjer: (ct + vt)∙(ct – vt) = (2ct')² = 2ct₁∙2ct₂)?
Zato jeste moguća ( i istinita je u fizičkoj stvarnosti, može se eksperimentalno provjeriti i utvrditi ) matematička relacija: (c + v)/2c = (t₁/t)² = cos²α/2; kao i relacija: (c –v)/2c = (t₂/t)² = sin²α/2.
Nemoj me samo pitati: „A šta ti je ...“, jer sam nekoliko puta napomenuo: Kada prvi put upotrijebim neku oznaku i definišem je, onda ta oznaka (sa prvobitnom definicijom) ostaje važeća u svim mogućim slučajevima (koje ću i kasnije navoditi). Ona jednačina E. L. Kronekera ima veze sa ovim istinama ( a ona važi za svako t) i tačna je za svako 0<v<c.


_{[Ovu poruku je menjao Sprečo dana 12.12.2004. u 14:59 GMT+1]}

Ne znam na šta misliš. Da li bi mogao da daš neki link na citat na koji misliš, pa da vidim šta je u pitanju?

---

Želim Vam (svima) veselu Novu godinu i sretnu 2005. godinu! Na ovo me ponukao prijedlog Cibernoidu da do Nove godine okončamo MM-eksperiment. Cibernoid, kada smo, ono bili zajedno u K₀ i sinhronizovali „satove“, „etalone“, utvrdili talasnu dužinu i frekvenciju svjetlosti, Nedeljko ispali „startni pištolj“ i...krenuše sferni talas brzinom c i K' brzinom v. Čvrsto vezano za K' (y-osa) stoji naš „etalon“ l₀ = ct₀ = PO₂ = 11m („računajući mnogobrojne refleksije“) i može se mikrometarskim zavrtnjem birati položaj „ravani ogledala“ tako da se odbijeni talas usmjeri u željenom smjeru. Računajmo i mi kao da c ima brzinu 3∙10₈m/s i da brzina v ima vrijednost 3∙10⁴m/s. Položaj ravni „okomitog ogledala“ bio je paralelan x-osi tako da je (upadni ugao jednak odbojnom) sferni talas stigao do ogledala (O₂) nakon vremenskog intervala t' , prešavši optički dužinu puta ct' = . Sprečo se ovdje poslužio „šarmom“ ( ne „kvarkom“) i „bio prisutan“ tačno uz ogledalo, da vidi šta se to u ovom momentu zbiva i događa. Kakvog li „iznenađenja“, ni djelić one „talasne dužine“ ne odbi se u smjeru tako da pogodi onu prizmu na x-osi, već čitava sljedeća „talasna dužina“ prođe mimo durbina. U momentu kada onaj „djelić“ iz „okomitog kretanja“ stiže do prizme (P') na x-osi, odbijeni talas od ogledala (O₁ na x-osi nije bio „ni blizu“ prizme (nema superponiranja, nema interferencije). Nešto malo kasnije pristiže i onaj Franjo iz „paralelnog kretanja“ u prizmu (pa u durbin ode sam samcat, nema one njegove „gornje polovine“ da mu se pridruži, previše se „raskoračio“). Ovo je tek „prvi čin“ predstave. U „drugom činu“ ja se „šćućurio“ uz K' i posmatram šta ze zbiva kad onaj F – paralelni, ulazi u prizmu (nisam ni ja „stao“, već mu prilazio brzinom v).

Ne vidim kako to crtez i formule na papiru mogu da uticu na ponasanje instrumenata. U fizici se radi obrnuto, jednacine
i crtezi se ordedjuju na osnovu eksperimentalnih podataka.evo animacije
Ako pokusavas da objasnis nepromenljivost slike izostankom interferencije, zao mi je,to nije validno objasnjenje.
U MM eksperimentu interferenciona slika uvek postoji samo se njen konkretan oblik sara menja u zavisnosi od fazne razike dva pristigla talasa.
evo slike

---

Ne, ne , ne u drugom smjeru (ja sam „kriv“ što sam želio pokazati u kakve detalje sam se upuštao). Cibernoid, zadržimo se na onom mom – tvom „vagonu“ (metru, „etalonu“) i tvojim: „Ako misliš da li će moje izmereno l₀ imati istu brojnu vrednost kao i tvoje izmereno l₀, odgovor je ne“.... „...svak će izmeriti da onaj drugi ima „kraći“ vagon“...“Faza talasa će biti ista za sve, frekvencija i talasna dužina će za svakoga (ko se kreće različitom brzinom u odnosu na onog drugog) biti različita“....
Da bi se sporazumjeli, moramo imati neko zajedničko polazište. Prethodno smo: „sinhronizovali“ svoje satove, „etalone“, jedinice mjere, napravili iste instrumente i sve to provjerili prije nego što smo se našli „prostorno razdvojeni“, ja- K₀ i ti- K'. Šta sad (nakon „razdvajanja“) i dalje imamo jednako: zajednički prostor (istu razdaljinu u tom prostoru mjerimo K₀K' = K'K₀ brzinom c), instrumente i etalone, jedinice mjere, istu relativnu brzinu konstatujemo v, jednako PO (okomito postavljeno na pravac relativne brzine). Želio sam crtež samo ovog detalja: Trougao P₀O₂P', P₀O₂ = O₂P' = ct', P₀P' = 2vt'. To je slika samo jednog (beskonačno malog) trenutka. Već u sljedećem trenutku je nešto drugo (i sljedećim, naravno). Umjesto da ovu sliku posmatramo „apstraktno“ (pomoću svjetlosti i Majkelsonovog interferometra) možemo „zakonitost geometrije prostora i događaja u tom prostoru „ sasvim očigledno osmisliti i na prikladniji način posmatrati (usporiti film, na primjer). Gore navedeni izvodi tvojih misli slični su riječima mog komšije, vršnjaka (nikako da se usaglasimo, jer imamo različit način posmatranja i razmišljanja u startu). Sada ja tebi moram postaviti (slično kao što si ti meni) pitanje: Kako ćemo mjeriti razdaljinu K₀K', odnosno K'K₀ pomoću svjetlosnih signala? Moram pojasniti pitanje: da li ćemo slati (kratke) signale svakog sata (na primjer) ili neprekidan „tok fotona“?

Imamo razlicite orjentacije referentnih vektora, vreme za svakog od nas tece u
razlicitim pravcima. Svak ima svoje pravce levo, napred, gore i posle.
Moj pravac napred i tvoj pravac napred su dva razlicita pravca, moj pravac posle i tvoj pravac posle su dva razlicita pravca, zbog toga sto se mi krecemo jedan u odnosu na drugoga.
Kako? Zasto? Procitaj detaljno sta je AA rekao.

---

Našem akademiku (pokojni Ljolje Krunoslav) na pitanje: „Zašto ne koristiš + i – ispred drugog korijena“? – odgovorio sam: Priroda ne zna za + i – (desno, lijevo, gore, dolje), to je naša, ljudska, tvorevina. Priroda zna samo za progres (promjenu). Cibernoid, nikakvog uticaja na sadržaj događaja u prirodi nema naše gledanje (način posmatranja), ma šta Ajnštajn rekao. Ajnštajn je rekao: „Kamen putuje po pravcu u odnosu na koordinatni sistem čvrsto vezan sa željezničkim vagonom, a po paraboli u odnosu na sistem čvrsto vezan za tlo“, a ja dodao: „Ko prihvata Ajnštajnove izjave (tvrdnje) zdravo za gotovo, neka stane tačno iza ili ispred voza u kretanju, pa nek čvrsto stojeći na Zemlji skine gaće i duboko sagnut između svojih raširenih nogu posmatra putanju kamena i neka kaže šta će vidjeti: pravac, parabolu ili nešto treće“.
Način posmatranja (ili računanja) nema nikakvog uticaja na faktičko, prirodno stanje stvari i događaja, ali ima na naš spoznajni sadržaj, na naše relativne istine (da nam se nešto čini „kao da ima masu“, kao da će proteći (proteklo) vrijeme, kao da je dužina kraća, kao da je nešto bilo prije (a objektivno nije),...
Moram upotrijebiti silu iste skalarne vrijednosti (isti impuls) da bi nekoj masi dodijelio brzinu (v) unutar ma kojeg inercijalnog sistema (masa, sila, brzina), neovisno od brzine i pravca kretanja sistema, tako da je besmisleno uopšte pominjati pravac i smjer jednog sistema za opštije pojave od relativnog viđenja stvari iz ...u.... za...., kako posmatramo, kako mjerimo, šta vidimo (a nikako da se postavi pitanje:a šta ne vidimo, ne znamo, ne mjerimo, ne računamo,....). Eh, ti Ajnštajnovi, ne informisani posmatrači...
Dakla je (10.12.) postavio jako važno pitanje i ono ima veze sa Mmeksperimentom i načinom posmatranja i mjerenja. Mjeri to pomoću neprekidnog toka fotona ili pomoću prekinutih (morzeovskih) signala (ima to veze i sa onom pomenutom „stonogom“). Valja nam još dublje i preciznije posmatrati i vidjeti mnogo više.

Cibernoid, (šta nam je ovdje sporno), ukucaj tex ispred korijena u tvojoj poruci od 1o.12. (17^h i 15^min.), da bude formula „vidljivija“. Prema tvojim oznakama oba mjerimo istu dužinu 2l. Nesporazum, zato sam tražio da mi nacrtaš tu sliku.Upravo si naveo tipičan primjer „poturanja č...pod....g“. Čitavo vrijeme ja tu dužinu (koju ti „mjeriš“ i označavaš sa 2l) označavam sa 2ct' i striktno uslovljavam njenu „definisanost“ izmjerenom dužinom PO₂ = l₀ (koju smo „mjerili“ zajedno, istim jedinicama, instrumentima, u istim uslovima, zajedno je „postavili“ okomito na x-osu). Tvoje riječi govore o dužini 2K₀(0,0)PO₂(vt',l₀), a matematika o dužini 2l₀. Površno čitajući ovakve tekstove i olako baratajući sa upotrebom oznaka l₀, l' i l ne uvidimo gdje nas „govornom akrobatikom“ prebacuju iz jednog matematičkog sadržaja u drugi. To je ono što sam naglasio: nešto utvrdimo u jednim uslovima, a primjenjujemo isto to u drugim uslovima.

Drugi pokušaj da plasiram sliku.
Drugi pokušaj ubacivanja crteža:
[mg]



[/img]


_{[Ovu poruku je menjao Sprečo dana 16.12.2004. u 10:04 GMT+1]}

Evo te slike:

---

Ovu sliku sam želio vidjeti samo zbog sljedećih „činjenica“: A'A = 2ct i B'B= 2vt, te zbog tvrdnje da će omjer ct/vt = c/v = n ostati konstantan tokom širenja dva sferna talasa (ako im je širenje počelo istovremeno iz tačke P(0,0), PA = ct i PB = vt). Nedeljko je napomenuo da će za posmatrača u A' (koji „ne zna da se kreće“) tačka A „bježati“ brzinom (2c)∙t, a tačka P će se u odnosu na tog „posmatrača“ kretati brzinom c. U odnosu na posmatrača u P (koji takođe može smatrati da „miruje“) tačka A će se udaljavati, brzinom c (a sredina odsječka PA za tog istog posmatrača „bježat će“ brzinom c/2). Ako smo vrijeme t uslovili „događajima“ kao u MMeksperimentu: t₁ = i t₂ = , te t₁ + t₂ = t = , nda će za svako moguće 0<v<c biti: BA' = (ct + vt) = 2ct₁ i BA = (ct – vt) = 2ct₂. Tu nema „izuzetaka“ ( bilo kakvo l₀ izabrali i bilo koji par brzina 0<v<c koristili, ali je zgodno da tu zakonitost posmatramo isto tako dobro ako je c = 3∙10⁸m/s i v = 0,8c , (gdje je n = 5/4) i za neko drugo c i v istog omjera.

Da ne bi ispalo da „promovišem svoj rad“ (protivno pravilima ES-a) pitajte, komentarišite, diskutujmo, eventualno, sporne detalje. Ako nema primjedbi na prethodno izneseno (uvjerili ste se u tačnost za svako 0<l₀, i svako 0<v<c), onda da naglasim i važnost ct₁ – ct₂ = ct_v = vt = .
Oznaka t_v ima višestruko korisno „praktično“ značenje: Vezana je za brzinu v u jednako promjenljivim kretanjima, te za brzinu svjetlosti u „optički gušćim sredinama“ (v = c/n), lako se pamti smisao iz: ct_v = vt ili c/v = t/t_v = n, te kod jednako promjenljivih kretanja: a₀∙t_v] = v, a₀∙t∙t_v = vt = ct_v; ili kod impulsa (količine kretanja): F∙t_v = mv, F∙t = mc. U zavisnosti šta prvo definišemo („izmjerimo“, navedemo podatke) a šta izračunavamo uvijek ćemo imati veličine sa istim smislom, koje možemo isto označavati: l₀ = ct₀, t₁ = , t₂ = , t = t₁ + t₂, t_v = t₁ – t₂, t – t_v = ∆t, 0<v<c , bilo da govorimo o MMeksperimentu, prelamanju ili odbijanju svjetlosti, jednolikim (nepromjenljivim s obzirom na brzinu) ili jednako promjenljivim mehaničkim kretanjima (pravolinijskim ili kružnim), u trigonometriji, ....Sve se lako objašnjava, lako shvata i primjenjuje (korist višestruka).
No, vratimo se MMeksperimentu (da ne bi zaboravili na njega), jer je prikladan za lako objašnjenje Ajnštajnovih i Lorencovih istina.

Na novom crtežu (vidi poruku od 14.12., oznake nisu baš vidljive, nedostaje i K₀) u odnosu na prethodni dodao sam dvije koncentrične kružnice: PA = PA' = PN = ct i PB = PB' = PT = vt = ct_v i tri dužine: BN = AT = t = 2ct', te TT' = BT/n = 2vt', na x- osi tačka T' određuje dva odsječka poluprečnika PA = ct, tj dvije dužine: PT' = vt/n = ct/n² = vt_v i T'A = 2l₀. Rotacijom tačke T' (centar rotacije u P) na pravac kroz PN imat ćemo isto to i na poluprečniku PN = ct (ovo sam dodao zbog Cibernoidovog „pogleda“ iz B, jer će pod istim uglom vidjeti 2l₀ kao što ću i ja vidjeti dužinu BN iz K₀(0,0). Taj ugao APN = α ima vrijednosti trigonometrijskih veličina: cos α = vt/ct = vt'/ct' = vt₀/ct₀ i sin α = = , bez obzira o kojim se skalarnim vrijednostima brzina 0<v<c radilo, za koje je PA = ct i PB = vt. Lorencove formule za transformaciju koordinata vezane su za trigonometrijske vrijednosti polovine ugla α. Iz slike je očita jednakost: 2l₀/2ct'= 2ct'/ct = sin α. Ta istina nije rezervisana samo za brzinu svjetlosti c i neko v = c/n vezano za svjetlost, već i za svako o<v<c.

The American Institute of Physics Bulletin of Physics News Number 712 December 13, 2004 by Phillip F. Schewe, Ben Stein

IS SPECIAL RELATIVITY WRONG? The centennial of Albert Einstein's miracle year of 1905 has arrived and so it is pertinent to ask how one of his most famous theories is doing. Physicists don't necessarily believe that Einstein's rules about the nature of spacetime are mistaken, but as part of the continual scientific effort to extend what is known about the universe physicists search for subtle hints of a departure from expected behavior. Special relativity predicts that clocks traveling in various directions and with various fixed speeds relative to each other will tell time differently, but in such a way that spacetime has no preferred or distinguishable direction, a proposition known as Lorentz invariance. Physicists, always on the lookout for departures from received opinion, and also motivated by theoretical suggestions that such effects might be expected, take this as an invitation precisely to search for such a special direction or to find that the variation of clock rates does not adhere to Einstein's equations. Such effects are described by the "Standard-Model Extension" (SME) and they can come in several forms. One disproof of special relativity would be the finding that matter and antimatter behaved differently. Another would be a birefringence violation: observing that light with different polarizations travels at different velocities through vacuum. Still another disruption of the Einsteinian view would occur if the universe were pervaded by an underlying oriented energy field, one that interacted weakly with known particles so as to favor one direction over another.
A new experiment puts this latter violation to its most stringent test yet. As so often happens when searching for extremely subtle effects, no departure from known physics was found but a new upper bound could be established. Ronald Walsworth and his Harvard-Smithsonian colleagues, in conjunction with theorist Alan Kostelecky at Indiana University, look at how atoms prepared in special magnetic states (the precision of their light emissions allow them to serve as "clocks") vary in their timekeeping when moving at certain velocities (or "boosts") relative to the hypothetical Lorentz-symmetry-violating fields that may permeate the universe. In this case the two clocks consist of a sample of
helium-3 atoms and a sample of xenon-129 atoms held in a container within a fixed magnetic field. The clock rate in each case is the rate at which the atomic nuclei precess in the magnetic field. The emissions from one atomic species were fed into a feedback mechanism for controlling the magnetic field, so in effect the one set of atoms (or, to be more precise, their nuclear spins) acted as a reference clock while the other species served as the test clock.
The whole apparatus, and the absolute orientation of the applied magnetic field in spacetime (and along with it the orientation of the atoms and their emissions) change as the Earth rotates daily and as the Earth takes its annual course around the sun. Furthermore, to achieve the necessary level of precision (based on the light let loose by the atoms), the Harvard researchers achieved the difficult experimental feat of having the two atom samples operate in a maser mode (that is, they performed like a laser) within the same container. The existence of a Lorentz-violating field, one that like a magnetic field favors a particular orientation in an otherwise isotropic spacetime, could cause the two clocks to become more out of synch as they move relative to the Lorentz-violating field. The main result of the experiment was to put a stringent new limit on a coupling of material particles (primarily the neutron) to such fields. The upshot: no Lorentz "boost" violations are seen at a level of one part in 10^-27. (Cane et al., Physical Review Letters,
3 December 2004; previous relativity test summarized at http://www.aip.org/pnu/2003/split/623-2.html; contact Ron Walsworth at 617-495-7274, [email protected]; background articles in Physics Today, July 2004, Scientific American, Sept 04; Harvard website at www.cfa-www.harvard.eduWalsworth/Activities/DNGM/DNGM2.html;
Kosetlecky site,
http://www.physics.indiana.edu/~kostelec/faq.html#30 )

---

„Oprosti im, Bože, ne znaju šta rade“.
Većinu sadržaja (fizičkih, društvenih, socioloških, bioloških, psiholoških,...) u našoj objektivnoj stvarnosti umijemo protumačiti (bez obzira koliko to tumačenje bilo subjektivno i individualno – relativno). Što god smo dalje (prostorno, vremenski, sadržajno – spoznajno) od našeg „realnog svijeta“ sadržaje zbivanja (u mikro ili makro svijetu) sve manje razumijemo. Mnoge zakonitosti mikro i makro svijeta za nas su (bar za sada) nedokučive (zbog naše ograničenosti). Tumačiti pojave i zakonitosti naše objektivne stvarnosti zakonitostima makro – svijeta (i obratno; tumačiti naš realni i makro - svijet pojavama iz mikro svijeta) ne bi bilo uputno (veća vjerovatnoća da ćemo griješiti).
Ovdje pričamo o promjenama, zakonitostima promjena u dvije dosta bliske oblasti fizičke stvarnosti (elektro-magnetne, te mehaničke promjene materijalnog svijeta) zajednički sadržaj u te dvije zasebne oblasti su prostor i vrijeme. Posmatranje promjena u prostoru i vremenu (te u prostoru ili vremenu ; neki se neće složiti da to možemo razdvojiti) možemo nazivati kretanje, ali moramo uočavati i sličnosti i razlike elektromagnetnih i mehaničkih kretanja (u prostoru i vremenu).
Primijenimo „božanski pogled“, na prostor i vrijeme. Pogledajmo taj Svemir kao da smo izvan njega, pogledajmo te njegove „individualne svjetove“ i zbivanja u njima. Za sada umijemo posebno izdvojiti na primjer Sunčev sistem i posmatrati to kao zaseban svijet. U tom Sunčevom sistemu možemo posmatrati pojedinačne svjetove, pa u tim pojedinačnim opet nove pojedinačne svjetove, i tako ići ma koliko možemo i umijemo u „mikrosvjetove“. Zbivanja u mikrosvijetu neće imati nikakvog uticaja na one svjetove „višeg ranga“ (raspad cjelokupnog svijeta jednog atoma nema nikakog uticaja na zbivanja i zakonitosti zbivanja Sunčevog sistema, bar to možemo zaključiti prema našim dosadašnjim spoznajama i iskustvima). Zato izvlačiti zaključke o prostoru i vremenu pomoću istina utvrđenih u mikrosvijetu (čije zakonitosti tek otkrivamo) za mene izgleda besmisleno.
Tekst ove poruke iniciran je prethodnom porukom (tek moram potražiti pomoć nekog ko zna Engleski), mogu samo pretpostaviti njen smisao i sadržaj (inače mi je intuicija jača od pameti).

Sprečo, zamisli vagon koji putuje brzinom v u odnosu na zemlju. U kupeu sedi putnik i vudu kako je foton sa lampe sa plafona visine L preleteo put do poda krećući se normalno ne njega brzinom c. Do pada fotona na pod prošlo je t=L/c vremena. Me]utim, železničar koji stoji pored pruge vidi isti tajfoton u kretanju koje nije normalno na pod, i pri čemu on prelazi put gde je t' vreme koje protekne od emitovanja fotona iz sijalice do njegovog pada na pod u očima železničara. Odatle jasno sledi da je Kako to objašnjavaš? Ovo je jedan od klasičnih primera, ali neoriginalnost neću prihvatiti kao argument protiv njega. Hoću da čujem šta tu ne valja.

---

Svjetlost, u fizičkom smislu, samo je djelić zasebnog „svijeta“ elektromagnetnih pojava ( i promjena). Uočene zakonitosti zbivanja u tom zasebnom svijetu pomažu nam da lakše i jednostavnije tumačimo i zakonitosti zbivanja u našem (realnom) svijetu.Konstantnost brzine svjetlosti u Euklidskom prostoru (prostor bez materije) pojmovno i sadržajno nimalo se ne razlikuje od konstantnosti brzine zvuka u homogenoj sredini (u metalnoj žici na primjer, ma šta radili sa tom žicom, nosili je ma kakvom brzinom u prostoru, mijenjali joj smjer i brzinu kretanja, okretali je ili savijali). Takav smisao ima Ajnštajnova primjena brzine svjetlosti, za svaki „zatvoreni sistem“ kao cjelinu (sistem je „nosač“ brzine svjetlosti). Da je to tako možemo se uvjeriti primjenom te istine na uočena kretanja u MMeksperimentu ili na Lorencove jednačine za transformaciju koordinata („prelaz iz sistema u sistem“). Da bi se mogli (sami) u to uvjeriti nije dovoljno „Sprečine“ matematičke istine samo pročitati, već se treba prihvatiti olovke pa računati i provjeravati sve ono (i još mnogo više) što sam naveo za A'A = 2ct i B'B = 2vt i tačkom P(0,0) kao zajedničkom sredinom te dvije dužine. Namjerno sam upotrijebio vrijednost za v = 0,8c zbog istog takvog primjera na web stranici M. Miloševića i istog takvog primjera korištenog ranije na ovom Forumu (Nedeljkov proračun).
Tek sad sam pročitao Nedeljkovu poruku (tek ću je razmotriti).

Ne, konstantnost brzine svetlosti u TR nije isto što i konstantnost brzine zvuka u nekoj homogenoj sredini jer se tu ne radi o istoj "konstantnosti". Konstantnost brzine svetlosti znači da se svetlost prostire u svim pravcima istom brzinom nezavisno od uzajamnog kretanja izvora i prijemnika svetlosti. Recimo, kada sirena voza zapišti daleko od nas, mi ćemo pre čuti taj signal ako trčimo u susret sireni, nego ako stojimo u mestu. Ovde se govori o relativnom kretanju u odnosu na sredinu koja je nosilac prostiranja zvuka (vazduh). Drugim rečima, ako dva čoveka stoje na zemlji i sirena je na sredini puta između njih, i vetar duva od sirene ka jednom od njih, onda će taj čovek ranije čuti zvuk od onog drugog. U slučaju svetlosti toga nema. Napšominjem da ovde ne govorim o promeni visine tona (Doplerovom efektu), već o vremenu koje je zvuku potrebno da stigne do slušalaca.

---

Šta tu ne valja?
Prvo oznake. Dužinu od plafona do poda (po okomitom smjeru) mjerimo u K₀ u odnosu na K₀, dakle takvu dužinu će izmjeriti i putnik u vagonu (koji miruje u odnosu na vagon) i putnik koji je ostao na stanici ( na tome sam insistirao sa Cibernoidom kada sam želio „sinhronizovati satove, etalone za dužinu, masu, vrijeme,..., dakle sve smo uradili dok je „voz stajao“, zajedno i u istim uslovima, istim instrumentima i sve to u dovoljnom broju primjeraka). Kako dužinu „mjerimo“ u K₀ u odnosu na K₀ i označimo je sa l₀. Takva će biti i ostati i za jednog i za drugog, te tvoju prvu jednakost: t = L/c treba napisati: t₀ = l₀/c.
Kako si koristio oznaku t' za vrijeme onda tvoja druga jednakost treba da glasi:
l' = , što sam do sada napisao u različitim matematičkim iskazima, na različite načine (vezano za „okomito kretanje svjetlosti“ u MMeksperimentu). Konačno posljednja jednakost ima isti oblik kao i Ajnštajnova: t' = .
„Problem“ je sada šta se kome obistinjuje i u odnosu na šta se obistinjuje (odnosno u tumačenju toga šta se kome i u odnosu na šta obistinjuje, šta je stvarnost, a šta privid, šta „vidi“ a šta „ne vidi“). Zato sam insistirao da ovakve slučajeve analiziramo i sa brzinama c i v dostupnim očiglednijem posmatranju i provjeri navedenih geometrijskih i matematičkih istina (kako bi nam i sama „logika“ bila jasnija).
Tvoj navedeni primjer je potpuno analogan onom Cibernoidovom (samo „drugo poluvrijeme“), potpuno analogan „okomitom kretanju“ u MMeksperimentu od momenta kada je čelo talasnog fronta (koji je emitovan iz K₀(0,0) utrenutku kada su F , K₀ i K' bili u istoj tački P(0,0)) sustigao ogledalo O₂ (tada je Cibernoid bio tačno ispod tog ogledala, udaljen od koordinatnog početka P(0,0) za dužinu vt').
Dakle dok F (foton) ponovo ne sustigne od ogledala O₂ do Cibernoida (u njegovom „podnožju“) proteći će ponovo interval vremena t' (Cibernoid će se za to vrijeme pomjeriti za dužinu vt'). U startu ( u P(0,0) da Cibernoid ima mogućnosti vidjeti „čelo talasnog fronta“, Cibernoid bi vidjeo da mu se uz PO₂ „penje“ neka tačka do vrha, a zatim i nazad do dna (za njega po pravcu) brzinom (gore i nazad za vrijeme 2t').
Tvoj konkretan slučaj možemo bolje sagledati padanjem (prosječnom, srednjom, konstantnom,nepromjenljivom) brzinom c (od plafona do poda ) za neko vrijeme t₀ = l₀/c. Šta će vidjeti „posmatrač sa Zemlje“ (ako se vagon kreće brzinom v)? U ravni okomitoj na pravac kretanja imat će pravolinijsku putanju dužine (ct₀)² + (vt₀)² = ( l_x)².
Zaključak: U posljednjem primjeru i jednom i drugom će proteći vremenski interval t₀, a u gore navedenom primjeru i jednom i drugom će proteći vremenski interval t'. Tako će biti u svakom konkretnom slučaju. Vrijeme iskazano matematičkom jednakošću (izdvojeno na lijevoj strani jednakosti) obistinjuje se i jednom i drugom „posmatraču“. U tom smislu treba i bukvalno prihvatiti matematičku jednakost (lijeva strana jednaka desnoj strani, ma šta njome iskazivali, vrijeme, dužinu ili brzinu).
„Neoriginalnost“ kritikovao sam samo za to što si na sve što sam navodio servirao mi sadržaje koje sam davno iščitao, koji mi ništa ne znače. Ako sam napisao da je l₀ = t', onda treba baš to gledati i provjeravati, ne pričajući mi o „konkordu“ i ne navodeći mi ono što u većini udžbenika mogu naći (podrazumijeva se da sam to pročitao).