It is a remarkable(!) coincidence that
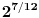
is very close to 3/2.
Why?
Harmony occurs in music when two pitches vibrate at frequencies in small integer ratios.
So, the equal-tempered scale (in common use today), popularized by Bach, sets out to "even out" the badness by making the frequency ratios the same between all 12 notes of the chromatic scale (the white and the black keys on a piano).
So to divide the ratio 2:1 from high C to middle C into 12 equal parts, we need to make the ratios between successive note frequencies
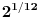
:1. The startling fact that
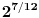
is very close to 3/2 ensures that the interval between C and G, which are 7 notes apart in the chromatic scale, sounds "almost" pure! Most people cannot tell the difference!
What a harmonious coincidence!
The Math Behind the Fact:
It is possible that our octave might be divided into something other than 12 equal parts if the above coincidence were not true!
It is worth noting that on a stringed instrument, a player has complete control over the frequency of notes. So she can produce pure harmonies.
There are a lot of interesting connections of mathematics with music. Take courses in music theory to learn more!
http://www.math.hmc.edu/funfacts/ffiles/10004.8.shtml