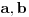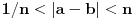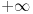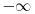Teorija Relativnosti

Mogao sam, ali nisam jer to nisi ni tražio pa sledi da se nisam izvukao niti sam imao potrebe za tim.

Kako gde? To ”gde” je tamo gde si rekao da se promatrač može kretati brzinom v većom od c i to uniformno.

Hvala ti – ako si mislio i na mene – a i ako nisi pridružujem se tvom čestitanju i svima želim samo jedno: da budu zadovoljni!


Ne, nije ti prvi put. Pogrešan koren je zato što mu je pogrešan radikand, a za to si odavno čuo, ali nisi znao.


Postavke STR su pogrešne i u suprotnosti sa aksiomom o jednakim posledicama jednakih uslova.

.
Možda bismo i odustali da ti nisi pokazao da se promatrač može kretati uniformno brzinom većom od c.


Na MM eksperiment!


Brzina svetlosti nije konstantna. Zaključak da je brzina svetlosti konstantna ne sledi iz rezultata eksperimenata. Ti rezultati su pogrešno protumačeni.
Eto to nije tako!

Meni ne treba ništa da radiš, nego ti treba da se koriguješ i da već jednom odgovoriš na pitanje šta se dešava kad se štap udaljava od promatrača.
Mene mrzi da računam, a tebe mrzi da crtaš “daleke predmete koji usporavaju” odnosno koji imaju negativno(?) ubrzanje


Pa Mara se kreće brzinom većom od c – to si ti rekao - i u tom trenutku može da sjaše sa svoje metle i kreće se uniformno tom brzinom.

Meni si rekao da sam se “izvukao” – a ovo nije izvlačenje nego besmislica. Otkud negativno ubrzanje bez delovanja sile?
Kod tebe više ne vazi ni zakon o inercijalnom kretanju.


Ubrzano ili uniformno kretanje po pravoj liniji, a ne po nekoj drugoj krivoj i to važi i za te ubrzane sisteme referencije.




Ovo je proizvoljna tvrdnja i bez ikakvog osnova. Mara i Jana se mogu jednako i nezavisno kretati u bilo kom sistemu, a ako se jednako
kreću onda prelaze jednake puteve, a jednaki putevi su međusobno jednaki za bilo koji pravolinijski referentni sistem, a to opet znači da
je odstojanje između Jane i Mare konstantno – koliko puta ti to moram reći?




Ništa tu nije OK. Ako se kupus brže ukiseli kad je toplo vreme onda možemo reći da vreme brže prolazi kad je toplo – i eto ti i formalizma i
interpretacije koji se na isti način primenjuju i u STR.
Teorija relativnosti je štetna teorija jer daje volšebna rešenja prirodnih procesa ne ulazeći u otkrivanje istinskih uzroka tih procesa.
Ona je unazadila a ponegde čak i blokirala istinski spoznajni postupak u otkrivanju stvarnih uzroka mnogih prirodnih pojava.

Ma, pomenuo si forum za matematiku, da sad treba da otvaram novu temu za to. Umesto toga si mogao u jednoj rečenici da kažeš koji su to principi, pa nisi. Odmah da ti kažem, obzirom da znam šta si svojevremeno lupao o realnim brojevima, ne verujem ti na reč da znaš zasnivanje matematike.



A gde sam to rekao? "Posmatrač" je metafora za prostorni koordinatni početak referentnog sistema, tako da u svom referentnom sistemu posmatrač svakako miruje. No, referentni sistem se uvek bira tako da prostorni koordinatni početak može biti materijalna tačka. Kada govorimo o više posmatrača, zapravo govorimo o više koordinatnih sistema od kojih je svaki referentan za nekog posmatrača, tj. posmatrači su zapravo, ono što je malopre navedeno.

STR isključuje kretanje materijalne tačke u odnosu na neubrzanog posmatrača (tj. u koordinatnom sistemu u kome važi I Njutnov zakon mehanike) ne može biti c ili veće.

Dakle, koji je citat sporan?



Rekao sam svima koji Novu Godinu slave po gregorijanskom kalendaru.



Je li to ova aksioma



Na nju sam već dao komentar, koji se koliko vidim, ignoriše.



Što se pogrešnosti tiče, ponavljam, problem je u tome što nerelativisti zapravo ne znaju šta tvrde, pa bez obzira na sve moje apeke, nikako da se izjasne o tome. Kada se raspravlja o protivrečnosti nekih principa, ne ulazi se u pitanje njihove "tačnosti" i "netačnosti", sve dok se ne izvede kontradikcija.



Niko ne brani Jani i Mari da imaju iste zakone ubrzanja u nekom ISR, ali to onda nije ondaj misaoni eksperiment, nego neki drugi. U tom drugom eksperimentu imaćemo drugačije zaključke. Drugi uslovi, drugi zaključci. Ako bi Jana i Mara imale iste zakone ubrzanja u nekom ISR, onda bi u tom ISR one imale konstantno rastojanje, ali bi se njihovo sopstveno rastojanje povećavalo, pa ne bi mogle da sede na fiksnim sedištima u istom neistegljivom avionu, osim da sede na istom sedištu (jedna da sedne drugoj u krilo), a konstantnost sopstvenog rastojanja je uslov iz tvog misaonog eksperimenta.

Sledeća tri zakona nisu uzajamno nezavisna:

1. Zakon kretanja Jane.
2. Zakon kretanja Mare.
3. Zakon njihovog sopstvenog rastojanja.

Ti si hteo to troje da izabereš, a u tom slučaju nemaš garanciju korektnosti misaonog eksperimenta, kao kada bi u misaonom eksperimentu kupovine u radnji zadavao koliko je kupac dao novca, koliki je kusur i kolika je cena robe. Zadaj dvoje od to troje, a ono treće računaj.



O ovome može da se raspravlja kada se raspravi pitanje protivrečnosti STR. Jedan od načina je da odustanete, pa da pređemo na drugu temu. Isto važi za MM eksperiment.



Tebe mrzi da računaš, pa si našao mene budalu kao roba. To neće moći.



U trenutku "sjahavanja", Mara ima prekid u zakonu ubrzanja. Već si rekao da prihvataš da se ubrzanja menjaju postepeno. Uostalom, ako Mara ima brzinu, ona u toj rečenici nije posmatrač, već posmatrani objekat, a ovakve brzine su posledica ubrzanja posmatrača.



Naravno da ne važi u ubrzanom sistemu, jer inače ne bi bio ubrzan, već inercijalan.

Na ostatak ću odgovoriti kasnije.

---

Znači, pavolinijski referentni sistemi su ubrzano ili uniformno kretanje po pravoj liniji. Sad se mešaju pojmovi kretanja i referentnog sistema. Divno. No, da zanemarimo to što ova rečenica ne znači ništa. Ako bi se našao u otkačenom liftu i gurnuo neki predmet horizontalno, video bi da se taj predmet kreće pravolinijski. Posmatrač iz zgrade bi pak, po klasičnoj mehanici, video paraboličnu putanju. Koja je linija prava nezavisno od izbora koordinatnog sistema?



Teorija koju si naveo opisuje samo brzinu kiseljenja kupusa u zavisnosti od temperature. Ako si pak mislio da opišeš i mehaničke pojave, onda ti treba definicija vremena u kojoj važi npr. zakon održanja impulsa.

Daleko od toga da sam u STR video takve volšebnosti.

---

Tvoje verovanje nije važno. Važno je da si saznao kakva je uloga matematike u fizici. Što se tiče „lupetanja“ ono se prvenstveno odnosi na tvoj stav da
funkcije imaju vrednost i kad ne postoji argument, besmislenu tvrdnju da je tačka gradivni element dužine, da je kvocjent nekog broja sa beskonačnom
vrednošću jednak razlici dvaju jednakih brojeva, o odnosima među nulama i t. d. a o besmislenom dokazivanju nekih tvrdnji uz pomoć bijekcije bi tek
trebalo da te preslišam, ali rekosmo – ovo nije forum za matematiku.

Ko je tvrdio drukčije? Ako promatrač sedi na raketi on je u ubrzanom pravolinijskom referentnom sistemu i u njemu miruje. Ili, možda, po tebi, ubrzani referentni
sistem ne može postojati?

Ovaj:

A ovo je već lov u mutnom. Tu smo govorili o ubrzavanju štapa, a ne promatrača. EVO:

Rekao sam da prihvatam postepeno smanjivanje ubrzanja, ali to ne znači da se smanjuju brzine već naprotiv – one se uvećavaju dok god postoji imalo ubrzanja –
ili to možda ne shvataš. U trenutku sjahavanja Mara već ima brzinu veću od c i dalje se kreće po zakonu inercije tom brzinom – uniformno, ako priznaš zakon
inercije – jer ona više nema veze sa „metlom“ niti joj se više smanjuje brzina.

Dao si, ali on je u suprotnosti sa aksiomom o jednakim uslovima.

Šta će ti ISR? Jana i Mara imaju jednak potisak u smeru njihovog odstojanja i to je sve što definiše njihovo kretanje u bilo kom pravolinijskom referentnom sistemu.
Bilo kakva tvoja promena ubrzanja ili odstojanja je u suprotnosti sa početnim uslovima i sa aksiomom o jednakim uslovima. Tri „zakona“ koja pominješ su zavisna
samo od jednakosti početnih uslova.

Taj način bi ti trebalo da usvojiš jer je očigledno da ti nešto ne ide.

Tražio sam da razmišljaš, a ne da računaš, a sa računicom ništa nisi ni pokazao ni dokazao.Tebe mrzi da crtaš, a i za nacrtano ti treba pomoć.

Pa nisi razumeo. Radi se o međusobnoj jednakosti puteva. Ja bih gurnuo još jedan predmet istovremeno i za mene bi oba predmeta prelazila jednake puteve
i bila bi na istom odstojanju, a za promatrača iz zgrade bi oba parabolična puta bila jednaka i na istom odstojanju. Jednake stvari pod jednakim uslovima
izgledaju međusobno jednako, pod drugim uslovima izgledaju drukčije, ali međusobna jednakost tih izgleda je opet jednaka. Ni u jednom pravolinijskom
referentnom sistemu ne može put jednog predmeta izgledati drukčije od puta drugog predmeta ma kakav bio izgled tih puteva.

U konkretnom slučaju ja padam po pravoj liniji ubrzano i to je moj referentni sistem, za promatrača u zgradi bismo mogli reći da je u inercijalnom sistemu –
ali ako nam je, na primer, ringišpil referentni sistem onda se stvari komplikuju jer to više nije pravolinijski referentni sistem.

Bravo! To je pravi odgovor. Biće od tebe nešto kad se otkačiš od STR.

Što se tiče funkcije, voleo bih da vidim link na ovo sa funkcijama da bih video o čemu se zapravo radi.

Duž jeste skup svih tačaka koje se na njoj nalaze. Polazni pojmovi u matematici su skup, relacija pripadanja skupu i jednakost skupova (ovo treće se, doduše, može svesti na na prethodna dva), a svi ostali pojmovi se definišu preko ovih polaznih. Definiciju "gradivnog elementa" nikada nisam ni video ni čuo, ali znam šta je element skupa. Dužina je sa druge strane broj pridružen nekoj krivoj.

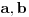
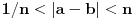
Što se količnika tiče, ima bar tri zasnivanja analize: standardna, nestandardna i glatka infinitezimalna. Prva se zasniva na polju realnih brojeva kao kompletnom uređenom polju, a teorema je da u kompletnom uređenom polju nema ni beskonačno velike ni beskonačno male veličine. Za ma koje različite elemente postoji prirodan (dakle, konačan) broj takav da je . Međutim, zbog lakšeg rada uvodi se i tzv. 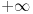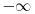prošireni skup realnih brojeva konstantama i , pri čemu ne možeš da vršiš bilo kakve operacije nad bilo kojiem elementima proširenog skupa realnih brojeva. Preciznije, prošireni skup realnih brojeva ne obrazuje polje. No, količnik konačnog i bilo kojeg od dva beskonačna elementa se definiše kao 0, a 0 je razlika bilo kojih konačnih jednakih vrednosti ( nije definisano) i razlika nejedankih vrdnosti nije 0.

U drugom zasnivanju analize imaš i beskonačno male i beskonačno velike veličine, ali se te beskonačno male veličine nikako ne zovu "nulama", jer je nula neutral za sabiranje, a u polju imaš tačno jedan neutral za sabiranje. Korektan rad sa svime time je složeniji nego što si ti svojevremeno pisao, te se iz tog razloga i ne radi na fakultetime, osim u vidu izbornog predmeta. Nije dovoljno uvesti jednu infinitezimalu, pa je množiti konačnim veličinama, stepenovati itd. Konstrukcija je složenija i izvodi se preko tzv. ultrastepena. Za konstrukciju ti treba neglavni ultrafilter nad skupom prirodnih brojeva, koji ne možeš da konstruišeš, već samo posredno da dokažeš njegovo postojanje, tako da eksplicitna konstrukcija takvog ultrastepena zapravo nije ni moguća.

U trećem zasnivanju analize se dopušta rad sa beskonačno malim veličinama, mada ih nema u eksplicitnom obliku. Beskonačno male veličine se u tom slučaju definišu kao veličine različite od nule, čiji je neki stepen (npr. kvadrat) jednak nuli. U polju takvi elementi ne mogu da postoje, pa zato iskaz "postoji bar jedna infinitezimala" nije teorema tog sistema. Za razumevanje tog koncepta je neophodno poznavanje intuicionističke logike, a za dokaz neprotivrečnosti takve teorije mnogo više (intuicionistički topos modeli).

Mogu ja da shvatim da neko pravi neko novo zasnivanje. Međutim, kritikovanje nečega što neko nije nikada ni upoznao je u najmanju ruku besmisleno, ako ne i bezobrazno. Ako pak neko ponudi neko svoje zasnivanje, onda mora jasno da ga formuliše (preko aksioma ili preko modela). Reći "ovaj zadatak se radi ovako" jednostavno nije dovoljno, tako da su se iz svega što si pisao videli samo neznanje, bezobrazluk i oholost.

Što se nula tiče, kao što već rekoh, u polju imaš tačno jednu. Ali šta vredi tebi pisati, kada ne znaš ni šta je polje. Ne uči se matematika iz poruka, već iz debelih knjiga.

A što se bijekcije tiče, matematika je neumoljiva. Ima svoja pravila po kojima proizvodi teoreme, sviđale se one nekome ili ne. To što neko smatra neki stav "besmislenim" ne znači da taj stav nije matematička teorema. Stavodi se prihvataju na osnovu korektnosti dokaza, a ne na osnovu odgovaranja našoj intuiciji i "sviđanja". Isto važi i za dokaze. Bitno je da li je izveden po matematičkim pravilima, a ne da li se nekome sviđa. Reč "besmisleno" se obično upotrebljava kada nešto ne odgovara nečijim shvatanjima. Reč "nekorektno" se pak upotrebljava kada za konkretan korak možeš da utvrdiš da nije po pravilima. Ali, za to treba znati pravila.



Opet se pozivaš na pojam "pravolinijskog" referentnog sistema, za koji sam rekao zašto je problematičan, ali ko mene šiša.



U odnosu na šta?



Ako Jana posmatra Maru, smanjenjem ubrzanja Jane će se Marina brzina u Janinom sistemu smanjivati. O tome se radi. U velikoj sam dilemi da li uopšte da nastavljam raspravu dok ne proučiš one formule, jer ovako nema svrhe.



Čak i ako je tako, šta me briga - tvoj aksiom je tvoj problem.

No, Jana i Mara u Janinom sistemu imaju iste zakone brzina (pa, samim tim i ubrzanja) - miruju, pa im je rastojanje u tom sistemu konstantno. Njihovo rastojanje je nekonstantno u referentnom sistemu zemlje, a u njemu Jana i Mara nemaju iste zakone ubrzanja. U prethodnom eksperimentu sa dva aviona su zakoni brzina aviona bili isti u sistemu vezanom za zemlju, pa su u njemu imali konstantno rastojanje, dok njihovo sopstveno rastojanje nije isto, i u referentnom sistemu bilo kog aviona njihova ubrzanja nisu ista. U čemu je problem?



A šta to znači da "imaju potisak"? Nose li ga u tašnama? Kad ovo razjasniš, videćeš šta će ti referentni sistemi. Opet se pozivap na "pravolinijske" referentne sisteme.



Pa, početni uslovi su da nema ni brzine ni ubrzanja Jane i Mare u odnosu na pistu. I tako nam Jana i Mara ostadoše na pisti ravnopravne. Nema poletanja.

Da bi avion poleteo, mora postojati neka sila, a da bi postojala bar jedna sila, moraš imati bar jednu osnovnu silu. Usled gravitacione (o kojoj ne govorimo u STR) avion ne može poleteti. Elektromagnetne se plašiš. Ubiće te struja ako mi odgovoriš na pitanje o elektrodinamici. Jaka i slaba nuklearna, koliko znam, deo su standardnog modela, tako da možda i ne postoje u nerelativističkom obliku. Kako će tvoj avion da poleti?



Ne priznajem zakon inercije u ubrzanim referentnim sistemima. Na to sam već odgovorio. Toga nema ni u klasičnoj mehanici.



Meni ide dok ne izvedete kontradikciju, a kada je izvedete, onda će vama da ide.



Šta mi napriča. To mi kaže neko ko ne zna ni šta je kontradikcija, ni šta on sam zapravo tvrdi.



A ja od tebe tražim da ne postavljaš opet pitanja na koja je već odgovoreno. U sledećim porukama ćeš na sva pitanja na koja odgovor daju formule dobijati uniforman odgovor "vidi formule".



To nije bio primer za jednakost puteva, već za problematičnost pojma "pravolinijskog sistema". Ako je taj sistem vezan za lift pravolinijski, kako to da loptu koju komšija šutne po tlu sprata i koja se kreće pravolinijski, iz lifta vidiš da se kreće krivolinijski.

---

Ovo nije forum za matematiku, ali ako hoćeš, izjasni se pa da ti na forumu za matematiku pokažem i dokažem šta ja tvrdim.


A sad o sistemima:
Inercijalni sistemi se u odnosu na druge inercijalne sisteme kreću isključivo po pravoj liniji. Onaj u kom je promatrač zovemo još i referentnim.
Neinercijalni sistemi se u odnosu na inercijalne sisteme kreću po bilo kakvoj krivoj i jedna od tih krivih može biti i prava linija. Onaj u kom se
nalazi promatrač zovemo referentnim neinercijalnim sistemom. Ovo nauči i zapamti!
Dakle – šta je problematično kod pravolinijskog neinercijalnog referentnog sistema? Šta je problematično kod kružnog, eliptičnog ili nekog drugog
neinercijalnog referentnog sistema? U kakvom referentnom sistemu se nalazimo mi na Zemlji u odnosu na ostale planete?
Kakvi neinercijalni referentni sistemi mogu postojati po tvojoj nagruvanoj nauci?


Opet smicalica, pa u odnosu na promatrača.

AAAAA .... tu leži zec. Pa onda se postaraj da ga oboriš kao što je uradio Lobačevski sa Euklidovom.

Pa ti ne znaš ni šta je potisak! To je sila, Nedeljko, koja te gura da se krećeš ubrzano, a ubrzanje je promena brzine sa manje na veću.

Ne pomaže ti izvrdavanje. Ne jedan avion nego dva. Početni uslovi su : da su jednaki, da poleću istovremeno iz istog inercijalnog sistema,
da imaju jednak potisak, a posledice su da imaju jednako ubrzanje, da prelaze jednake puteve i da je rastojanje između njih konstantno.

Ako ti tvrdiš da promatrač iz jednog aviona vidi da se u toku ubrzanog kretanja onaj drugi avion od njega udaljava (“puca sajla”) onda
ti avioni ne prelaze jednake puteve, a to znači da nemaju isto ubrzanje, a to opet mora da znači da nemaju jednak potisak.
I eto ti izvođenja kontradikcije – ako se dešava ono što ti tvrdiš – negiraš početne uslove.

Te formule su samo matematička nadgradnja nad upravo dokazanom kontradikcijom.


Ovo je namerno podmetanje. Nigde nisam rekao da je izgled nekog puta jednak i nezavisan iz kog i kakvog se referentnog sistema promatra.
Govorio sam isključivo o međusobnoj jednakosti izgleda jednakih puteva iz bilo kakvog pravolinijskog referentog sistema.

Zar ne vidiš iz ovog tvog citata da bi i inercijalni sistem promatrača na Zemlji s jednakim pravom mogao nazvati „problematičnim”.
Nema problematičnih referentnih sistema – ista stvar se vidi različito iz različitih referentnih sistema, ali se međusobno jednake stvari
vide jednako iz svih pravolinijskih referentnih sistema. Obrati pažnju na reč : „međusobno”

I na kraju – pošto sam ti izveo kontradikciju koju si tražio – možemo da pređemo na prikaz nelogičkog matematičkog lupetanja u sračunavanju
puteva svetlosti u MM eksperimentu.

Pošto si ti taj koji tvrdi da svi ostali jedu goBna, pokretač teme bi trebao da budeš ti.



Inercijalni sistemi su u međusobnom ravnomernom pravolinijskom kretanju. Bilo neravnomerno, bilo krivolinijsko kretanje proizvodi ubrzanje. Takođe, možemo imati više posmatrača, tako da se o referentnosti sistema može govoriti samo ako se zna na kojeg se posmatrača misli.

Mogao bi da naučiš i zapamtiš da ne možeš govoriti o kretanju van konteksta koordinatnog sistema, a ne u apsolutnom smislu, jer apsolutno kretanje ne postoji ni u klasičnoj mehanici.



Problematična je definicija "pravolinijskog" koordinatnog sistema. Evo tvog odgovora na pitanje šta je pravolinijski koordinatni sistem:



Dakle, koordinatni sistem je kretanje! Alo, znaš li ti šta pričaš? Mešaš pojmove kretanja i koordinatnog sistema.



U pojmu ubrzanog (neinercijalnog) sistema nije ništa problematično. Problematična je samo definicija "pravolinijskog" sistema. Naravno, u ubrzanim sistemima ne važi zakon inercije.



Pročitaj pitanje na koje je ovo odgovor, pa odgovor na koji je bilo postavljeno to pitanje, pa odgovor na koji je to bio odgovor, pa kad budeš video kontekst, kašće ti se samo.

Ako je Jana ubrzani posmatrač koji posmatra daleku drugaricu Maru, Mara se približava Jani većom brzinom od c usled Janinog ubrzanja. Nije Marino sjahavanje sa metle releventno, već je Jana ta koja treba da sjaše, a onda će usled Janinog sjahavanja Mara usporiti u odnosu na Janu.

Mogla je ubrzana Jana da gleda u neubrzanog Miloša (zaljubila se). Sjahavao Miloš ili ne, isto mu se vata (zakon kretanja mu se ne menja, jer ionako nije bio ubrzan). Jana je ta koja treba da sjaše sa metle.



Opet stižemo do starog problema da zapravo ne znaš šta tvrdiš. Tvoj posao je da izvedeš kontradikciju držeći se samo STR i ničega više. Ja ne moram ništa da obaram, već samo da preispitujem korektnost tvojih izvođenja kontradikcije iz STR i nikakvi me principi koji nisu sastavni deo STR ne interesuju. Ako želiš da se pozivaš na neki dodatan princip, na tebi je da ga izvedeš iz STR. Tek onda imaš pravo da ga koristiš u izvođenju kontradikcije STR.

Vidiš, inženjeri i dan danas koriste euklidsku geometriju. Nisu znali da je "protivrečna". Ni Lobačevski ni bilo ko drugi nije oborio euklidsku geometriju, kao ni geometriju Lobačevskog. To su dva ravnopravna geometrijska sistema.



1. Pojam brzine je izveden iz pojma kretanja, koje je lancima vezano za pojam koordinatnog sistema. Naravno, sistem i kretanje nisu isto (kao što si napisao), ali se o kretanju može mgovoriti samo u kontekstu sistema, koji ovde ne vidim, ali baš nigde.

2. Koja sila kada u tvom "ošišanom" svemiru nemaš nijedan izvor sile? Evo šta je model tvog svemira:

Imaš konačan broj čestica bez dimenzija, koje se kreću u nekom izabranom inercijalnom sistemu S₀. Čestice se u njemu kreću ravnomerno pravolinijski, bez sudara i svaka čestica ima masu mirovanja. Inercijalni su oni sistemi koji se u odnosu na ovaj sistem kreću ravnomerno i pravolinijski, a ostali su neinercijalni. Inercijalni sistemi su povezani Lorencovim transformacijama, a mase čestica, koje ovde ne igraju nikakvu ulogu, se određuju po relativističnom obrascu preko mase mirovanja čestice i brzine čestice u razmatranom sistemu (inercijalnom ili neinercijalnom). U svim inercijalnim sistemima se čestice kreću ravnomerno i pravolinijski.

Ovo ti ostaje ako se odrekneš svih osnovnh sila, a obzirom da tada ni masa ne igra nikakvu ulogu, slobodno i nju možeš da zaboraviš. Znači imaš čistu kinematičku (da ne kažem geometrijsku) teoriju, bez traga fizike. Tako kako si krenuo bi trebao da pokažeš da ovakav model nije moguć.

Vidiš, Ajnštajn nije imao taj problem, već je još u prvom članku preko Maksvelovih jednačina imao elektromagnetnu silu, pa je i odgovarajući model bio bogatiji.



Koja sad dva aviona kad se Jana i Mara voze u istom?

Početni uslov je isto što i Košijev uslov za diferencijalne jednačine kojima se opisuju prirodni zakoni. U tvom svemiru su početni uslovi mase čestica (rekosmo da nisu bitne) i položaji i brzine čestica u istom trenutku u nekom sistemu (može i neinercijalnom). Kad to zadaš, onda pusti zakone izražene diferencijalnim jednačinama da dalje rade (izdvoje jedno rešenje zakona kretanja čestica) i nemoj da se mešaš. Obzirom da nemaš nijednu osnovnu silu, jedini zakon koji ti ostaje je da u inercijalnim sistemima čestice imaju konstantne vektore brzine, tj. vektor ubrzanja im je 0.



Opet pričaš o pređenim putevima van konteksta koordinatnog sistema. Pilot aviona se ne šeta po avionu, pa u sistemu aviona pilot ne prelazi nikakav put, npr.



Naravno da nema problematičnih referentnih sistema. Jedino što je problematično je definicija "pravolinijskog" sistema. Podsećam, definisao si ga kao kretanje, a ne kao koordinatni sistem. Ta definicija bi morala da se popravi.



Koju kontradikciju? Gde su tu dva isključujuća iskaza?

---

Nedeljko:
Mogao bi da naučiš i zapamtiš da ne možeš govoriti o kretanju van konteksta koordinatnog sistema, ...

Kretanje se proučavalo i opisivalo daleko prije rođenja Dekarta.Koordinatni sistem
je samo alatka koju možemo, ali i ne moramo koristiti.

---

Kao što kaže Milan – koordinatni sistemi su samo pomoćna stvar, a inercijalni ili neinecijalni sistemi su te pomoćne stvari vezani za neka tela
koja se mogu kreati u odnosu na druga tela ubrzano ili uniformno – dakle može se govoriti o kretanju nekih tela u odnosu na te pomoćne stvari
a isto tako u principu može se govoriti i o kretanju tih pomoćnih stvari u odnosu na neka tela. Toliko o tvom filozofiranju u vezi sa referentnim
sistemima. To u svakom slučaju nije predmet oko koga postoje bitno različita mišljenja.

Što se tiče Jane i Mare opet nešto izmišljaš. Kad smo uopšte govorili da Jana posmatra Maru jer si ti uvek govorio da su one u istom sistemu
bilo da su u avionu ili na štapu i da za njih nema promene njihovog odstojanja. Ali zanemari sve što smo rekli pa nacrtaj to što tvrdiš ili
zamoli nekoga da ti pomogne pa da to i vidimo.

Euklid je rekao da se kroz neku tačku van prave može povući samo jedna paralelna prava, a Lobačevski da može više. A sad ti kaži šta
ne valja ili kako treba popraviti moj aksiom o jednakim uslovima.

Tvoja priča o silama je skretanje sa teme, ali to neće moći – o tome možemo otvoriti posebnu temu – ali ne o silama nego o poljima sila koja se
pod odgovarajućim uslovima manifestuju kao kontinualne ili koncentrične sile.

Ni Koši ni Ajnštajn ne bi osporio mogućnost postojanja jednakih početnih uslova. To samo tebi može pasti napamet eda bi nekako spasio ono
što se spasiti ne može.

Vratio sam se na dva aviona zato što Janu i Maru muvaš po tvojoj volji a ne drugarski onako kako se dogovorimo.


Pa nije istina. Tebi treba sve nacrtati. Jesam li rekao da startuju iz istog inercijalnog sistema? Pa čak i da nisam rekao – ako se avioni međusobno
udaljavaju onda prelaze različite puteve u odnosu na bilo koje referentno telo ili bilo koji tvoj koordinatni sistem.
Stvarno si preterao, ali ništa ti to ne pomaže.

Kontradikcija je potpuno korektno izvedena.Ovi iskazi se isključuju:
1. Avioni su jednaki, startuju istovremeno iz istog inercijalnog sistema u istom smeru, imaju jednak potisak i kreću se kroz isti medijum i sve ostalo.
2. Razmak između aviona se povećava, avioni nemaju jednako ubrzanje ni brzine što znači da ne mogu prelaziti jednake puteve ni prema kom
referentnom telu ili sistemu.
Ili kraće:
a) Avioni su jednaki i kreću se pod jednakim uslovima
b) Avioni se različito kreću

Principijelno tvoja tvrdnja izgleda ovako: JEDNAKE POJAVE POD JEDNAKIM USLOVIMA DOGAĐAJU SE RAZLIČITO

OK, kojom si se brzinom kretao tokom kucanja ovog posta?



OK, kojom si se brzinom kretao tokom kucanja ovog posta?



Što se Mare tiče, ti si počeo da izmišljaš neke metle. Slažem se da to ne odgovara prvoj priči o njima. No, za to si ti kriv. Što se slika tiče, dao sam formule koje govore sve.



I ko je od njih dvojice u pravu?



Ne valja to što se u izvođenju kontradikcije u nekoj teoriji pozivaš na nešto što nije sastavni deo te teorije. Imaš pravo da koristiš kakve kod hoćeš principe koje prethodno izvedeš iz STR, ali tek kad ih izvedeš, a pošto si ti taj koji tvrdi da je ta teorija protivrečna, sav taj posao je na tebi. Moje je samo da proveravam korektnost izvođenja i isključivost iskaza.



Pa, ja to nisam ni osporavao, samo tvrdim da ono što si napisao nikako nisu početni uslovi, a iz naših početnih uslova sledi jedino da avioni ostadoše na pisti.



Udaljavanje je pojam izveden iz rastojanja, o kome se može govoriti samo u kontekstu koordinatnog sistema, a upravo o rastojanju govoriš u apsolutnom smislu. Pobogu, pa šta je kontrakcija dužina ako je rastojanje apsolutno?



Stavi tačku 2. u kontekst koordinatnog sistema, pa ćeš valjda videti.

U 1. je pomenuti inercijalni sistem vezan za zemlju i ako se cela tačka 1. odnosi na njega, onda je ta tačka u redu. Međutim, u tom koordinatnom sistemu je njihovo rastojanje konstantno i prelaze jednake puteve, pa svakako 2 ne važi u tom referentnom sistemu. Ono što se povećava je njihovo sopstveno rastojanje, što zbog kontrakcije dužina nikako ne može biti isto što i njihovo rastojanje u sistemu vezanom za zemlju. Dakle nekorektnost izvođenja je u nevođenju računa o koordinatnom sistemu u tački 2., tj.navođenju tačke 2. van konteksta koordinatnog sistema.

---

Pitanje je glupo. Onaj ko tebe uvažava mogao bi da kaže – izvini ali nisam video koordinatne sisteme pa ne znam.
Inercijalno kretanje možeš konstatovati samo u odnosu na druga tela, a ubrzano kretanje zbog delovanja neke sile
potiska možeš u nekim slučajevima konstatovati i bez toga, ali ti to verovatno ne razumeš. Neću da te zamaram.
Što se tiče Euklida – površan si – trebalo je da obratiš pažnju na reči „samo jedna” .
Što se tiče kontradikcije – tvoji principi iliti propisi me ne interesuju. Služim se isključivo logičkim zaključivanjem,
a tu su relativisti vrlo tanki. Po njihovoj “logici” avioni ne mogu da lete nikako akamoli jednako.

Rekao sam da je rastojanje za date uslove konstantno, a kontrakcija dužina je greška i to sam ti pokazao i dokazao.

Pa stavio sam - citiram sebe: ”... što znači da ne mogu prelaziti jednake puteve ni prema kom referentnom telu ili sistemu.”

Pa zar ti ne osećaš kakvu glupost braniš: sopstveno rastojanje aviona se povećava i upravo toliko je kontrahiranje
tog rastojanja za promatrača na Zemlji pa on uvek vidi konstantno rastojanje – dakle promatrač sa Zemlje uopšte
ne vidi šta se sa avionima dešava. O promeni sopstvenog rastojanja aviona on nema pojma ma koliko bilo njihovo
ubrzanje. Skrivena tajna za sve referentne sisteme izuzev za povlašćeni sistem jednog ili drugog pilota.

Ne Nedeljko, to nema veze ni sa stvarnošću ni sa logikom. Ovo je neumoljivo:

JEDNAKE STVARI POD JEDNAKIM USLOVIMA DOGAĐAJU SE JEDNAKO

A odatle nedvosmisleno sledi da ne može biti ni kontrakcije ni tvoje dilatacije.

Pa, neka je i glupo. Postoji li odgovor?



Pročitao sam, ali i dalje nema odgovora na pitanje ko je u pravu, Euklid ili Lobačevski.



Pa, u izvođenju kontradikcije u STR i ne bi trebalo da te interesuju moji ili Perini ili Žikini principi, već principi STR. Kada izvedeš kontradikciju oborio si principe koje si koristio. Naravno, barem jedan od njih. Ako si koristio neke svoje principe u izvođenju kontradikcije, onda upravo oni mogu biti uzrok kontradikcije. Uvedeš li svoje principe i izvedeš li kontradikciju, onda si samog sebe oborio. Zato se u izvođenju kontradikcije u nekoj teoriji koriste isključivo principi te teorije, da ništa drugo ne bi moglo biti uzrok kontradikcije.

Kažeš da si izveo kontradikciju služeći se isključivo logikom. Ako bi to bilo tačno, onda bismo imali protivrečnost u logici nevezano sa bilo kakvom fizikom.



Ne, nego po tvojoj logici odbacivanja svih osnovnih sila. Relativisti imaju kvantnu elektrodinamiku (zasnovanu na STR) koja obuhvata elektromagnetnu silu. Sa njom i kvantovanjem opisuje hemijske reakcije itd. - sve u svemu, sasvim dovoljno da se opiše rad bilo mlaznih bilo elisnih motora. Još imaju i standardni model, koji opisuje čak i rad nuklearnih motora. A imaju i OTR koja obuhvata gravitaciju i elektromagnetnu silu.



E, pa postoji sistem u kome je rastojanje konstantno i drugi sistem u kome se rastojanje povećava. U prvom su pređeni putevi isti, a u drugom različiti. Šta je tu sporno? Imaš jedan sistem u kome su pređeni putevi isti i drugi sistem u kome se rastojanje povećava. Da je reč o istom sistemu, to bi bila kontradikcija, ali reč je o različitim sistemima i zato nemaš kontradikciju. Ne postoji nijedan sistem u kome je cela tačka 2 ispunjena, već jedan u kome je prvi deo ispunjen i drugi u kome je drugi deo ispunjen.



Drago mi je da si shvatio iskaz koji zastupam. Jedino mi nije jasno zašto je to glupost.



STR predviđa da je dužina štapa najveća u onom sistemu u kome on miruje, a ista je tolika i u sistemima koji se kreću u odnosu na štap po pravcu normalnom na štap. U ostalim sistemima je manja. Šta je tu problematično?



Šta bi sa loptom koja se za jednog posmatrača kreće pravolinijski, a za drugog po paraboli?

ISTA POJAVA MOŽE DA IZGLEDA RAZLIČITO U RAZLIČITIM SISTEMIMA[/quote]



Pazi samo da odatle ne sledi 0=1.

---

Što se realnih brojeva tiče, možeš da posetiš forum za matematiku. Ima novosti.

---

Ako sam ne vidiš odgovor džabe je da ti ga bilo ko da.

Ma nemoj mi reći – alal ti logika!
Mika, Pera i Laza su rođeni kao trojke. Mika liči na Lazu i Pera liči na Lazu, ali po tvojoj tvrdoglavoj tvrdnji (STR) Mika i Pera
ne liče pa ne liče. Ja onda uvedem “svoj” princip koji glasi: Ako su dve stvari slične trećoj onda su i međusobno slične. Na
osnovu toga principa tvrdim da ti nisi u pravu i da je tvoja tvrdnja u kontradikciji sa mojim principom. Oborio sam tebe, a ne
samog sebe. I šta je važno čiji je princip ako je tačan? Pričaš bajke.

Opet neistina – to nigde i nikad nisam učinio. Ti sebi svašta dozvoljavaš. Rekao sam samo da potisne sile bilo kakvih avionskih
motora mogu biti jednake.

Sporno je to što je ta tvrdnja u suprotnosti sa aksiomom o MEĐUSOBNOJ JEDNAKOSTI jednakih stvari u bilo kom ISR
Ako su, na primer, dve duži jednake i paralelne i nalaze se u određenom ISR, onda su one MEĐUSOBNO jednake i
paralelne i u bilo kom drugom pravolinijskom SR s tim što obe mogu biti kraće zavisno od ugla iz kojeg ih promatramo, ali
uvek MEĐUSOBNO jednake i paralelne. Zato je to što ti braniš glupost. Pokušaj da ukapiraš!

AKO SU POJAVE JEDNAKE, ONDA SU ONE MEĐUSOBNO JEDNAKE ZA BILO KOJI PRAVOLINIJSKI SISTEM REFERENCIJE.

Problematično je smanjivanje.

Slabo te služi pamćenje. Odgovorio sam ti na ovo pitanje baš kao i ti ovim:
ISTA POJAVA MOŽE DA IZGLEDA RAZLIČITO U RAZLIČITIM SISTEMIMA
Ovo je apsolutno tačno ako je u pitanju izgled – slažem se u potpunosti – ali nije u suprotnosti (kontradikciji) sa ovim:
AKO SU POJAVE JEDNAKE, ONDA SU ONE MEĐUSOBNO JEDNAKE ZA BILO KOJI PRAVOLINIJSKI SISTEM REFERENCIJE.
Jednake pojave mogu izgledati različito u različitim sistemima, ali ne i međusobno različito. Udubi se malo u ovo!

TO odatle ne sledi kao ni OVO: a – a = a/beskonaćno = 0.
TO sledi iz STR Pomogao si mi. Međusobno kretanje u jednom referentnom sistemu = međusobno mirovanje u drugom.

Stara dobra metoda izvlačenja.



Ovde ne vredi ni raspravljati. Čovek izvede kontradikciju iz T+P (mada ni to nisam video kako treba) i iz toga tvrdi da nije T. Kažeš mu i on tera dalje. Tim metodom možeš "oboriti" svaku teoriju uvodeći novu aksiomu 0=1. Neka je G bilo koji tvoj iskaz i A aksioma 0=1. G+A je svakako protivrečno, pa dakle tvoj iskaz G nije tačan. Možeš li da prihvatiš primenu iste "metode obaranja" na tvoje iskaze? Ako budeš ovako terao dalje, ja bataljujem dalju diskusiju, jer bez poštovanja osnovnih pravila logike argumentovana diskusija nije ni moguća.



Ovo mi se sviđa. Aksioma zapravo glasi: svaka binarna relacija je tranzitivna. Primeni to na sledeću relaciju sličnosti: ljudi su slični ako im se broj vlasi kose razlikuje za najviše 1. Mika ima n vlasi, Laza n+1, a Pera n+2 vlasi. Mika i Pera su svakako slični Lazi. No, pošto po tvojoj akskiomi onda moraju i Mika i Pera biti slični, dolazimo do toga da je . Uvođenjem ovakvih principa uvek možeš da izvedeš kontradikciju.



Ako izvedeš kontradikciju iz A+B i dokažeš B (korišćenjem eventualno logike i pretpostavke A), onda si oborio A. Da, ako iz logike + STR izvedeš neki princip, slobodno ga koristi u izvođenju protivrečnosti STR.



Jesi. Uporno si odbijao da odgovoriš na pitanje kako bi uveo elektromagnetnu silu. OK, mogu ja da razumem antirelativiste da se plaše da ih ne ubije struja, ali nisi dao nijedan drugi izvor sile. Potisne sile motora moraju imati izvor. Ako nema izvora sila, ne može biti ni sila, nikakvih, pa ni potisnih od motora. U takvom svetu i jesu sve sile jednake - nuli.



Sporan je pojam pravolinijskog sistema referencije. Definisao si ga kao pravolinijsko kretanje i nisi se nigde korigovao. OK, prihvatiću to da pravolinijski sistem referencije nije sistem referencije, nego kretanje i izvršiti odgovarajuće zamene u tvom iskazu



Šta to znači da su duži jednake i paralelne u nekom kretanju? Šta znači da su pojave jednake za neko kretanje? Ove rečenice nemaju nikakvog smisla.

Razumeš li ti šta je kretanje (promena položaja nečega u vremenu) a šta koordinatni sistem (sistem predstavljanja prostorvremenskih tačaka brojevima) i koje si dve stvari izjednačio?



Zašto?



Međusobno kretanje jednog tela u odnosu na drugo podrazumeva kretanje prvog u koordinatnom sistemu u kome drugo telo miruje, a ne rastojanje u proizvoljnom sistemu. Ovo je tačno:

Iz STR sledi da dva tela koja imaju konstantno rastojanje u jednom inercijalnom sistemu, mogu imati nekonstantno rastojanje u nekom neinercijalnom sistemu.

Kao i

Iz STR sledi da dva tela koja imaju nekonstantno rastojanje u jednom inercijalnom sistemu, mogu imati konstantno rastojanje u nekom neinercijalnom sistemu.

---

Takvim aksiomima se ti služiš!

Što bih primenjivao takvu relaciju koju ti primenjuješ– ima i relacija apsolutne sličnosti.

0=1 ili kretanje = mirovanje i to sam i koristio u izvođenju protivrečnosti.

Nisam niti me interesuje priroda sila i to nije tema – važno je da postoje potisne sile i da su jednake. Sve ostalo ti je priča bez potrebe i skretanje
sa teme.

Znam da ti ovaj sistem zadaje glavobolju ali ako ga tobože ne razumeš – veži ga za referentno telo koje se kreće ubrzano po pravcu.

O da – imaju itekako smisla – pređeni putevi su takve duži i one su jednake za jednake avione.

Razumem, a ti?

Zato što upravo o tome i raspravljamo!

Nema šanse!

Bilo bi dobro, na primer, da nam kažeš iz kakvog referentnog sistema bi se neke dve zvezde, koje su
na konstantnom rastojanju, međusobno približavale. Opiši nam taj referentni sistem. Budi ljubazan.

Gde to leba ti? Drugo, po čemu ti možeš da uvodiš neke aksiome, koje nemaju veze sa STR u obaranju STR, a ja ne mogu da uvodim aksiome u obaranju tvojih iskaza?



Zato što si uveo neki princip za relaciju sličnosti, koju niti si definisao, niti si zadao bilo kakav uslov za nju. Znači, princip se primenjuje na bilo koju binarnu relaciju.



Pa, ako si koristio 0=1 ili kretanje = mirovanje, onda je to uzrok protivrečnosti. Za to ti ne treba STR. Iz toga je vrlo lako izvesti protivrečnost. No, to onda ne znači da je STR protivrečna.



U, itekako si sa podsmehom odbacio razmatranje elektrodinamike, a to nije da baš nema veze sa temom, jer je upravo elektrodinamika problem koji nerelativisti nisu uspeli da reše. No, niko ti ne brani da pokušaš da izvedeš kontradikciju iz STR bez pozivanja na Maksvelove jednačine. Prirodu sila sam morao da pomenem kada si počeo da pričaš o "posledicama početnih uslova". U našem slučaju je početni uslov stajanje aviona na pisti i jedina posledica tog početnog uslova je da avioni ostadoše na pisti, budući da izvora sila nema.



Ako sam dobro razumeo, pravolinijski sistem je sistem koji se kreće pravolinijski u odnosu na bar jedan inercijalan sistem. To je već čista i jasna definicija sa kojom se može raditi.

No, u tom slučaju se taj sistem kreće krivolinijski u odnosu na neki drugi inercijalni sistem. Zamisli sistem S vezan za lift koji se otkačio. On je pravolinijski jer se kreće pravoj liniji u odnosu na inercijalni sistem zemlje. Zamisli sada sistem S' vezan za biciklistu koji se kreće po zemlji ravnomerno i pravolinijski. Sistem S' je inercijalan jer se kreće ravnomerno pravolinijski u odnosu na inercijalni sistem zemlje. Međutim, pravolinijski sistem S se kreće krivolinijski u odnosu na inercijalni sistem S'.



Nije bitna jednakost aviona, već jednakost početnih brzina i zakona ubrzanja. No, o tome ima smisla govoriti samo u kontekstu koordinatnog sistema.

1. U sistemu vezanom za zemlju su ti parametri isti i pređeni putevi su isti.
2. U sistemu vezanom za jedan od aviona, ti parametri su različiti i pređeni putevi su različiti.

Ako pak govoriš o sopstvenom ubrzanju aviona (koje osećaju piloti), početnim brzinama u odnosu na zemlju i pređenim putevima u odnosu na repere na zemlji, onda su parametri jednaki i pređeni putevi su jednaki. To to je tačka 1. (merenje parametara u odnosu na zemlju). Ako pitamo pilote kolike su puteve prešli, da dobićeš jednake izveštaje. To nije sporno. No, to nije u suprotnosti sa povećavanjem sopstvenog rastojanja, jer jedno je ubrzanje koje pilot A oseća, a drugo je izveštaj pilota B o ubrzanju pilota A.



Nešto je problematično zato što raspravljamo o tome. Zanimljivo. Znači problematično je sve o čemu iko raspravlja.



Krećeš se ubrzano po pravcu tih dveju zvezda, a nisi između tih zvezda.

---

Evo: relativno kretanje između dva tela ne može se konstatovati. To je tvoj aksiom, a moji su istiniti.

Ako bismo sve opisivali u tančine trebalo bi nam mnogo više i vremena i prostora – a ti se vataš za dlake.

Znači - jer po tebi ona tvrdi da je 0 =1 odnosno relativno kretanje= mirovanje.

Nisu ni relativisti.

Sve se tu podrazumeva a ovo je tvoja 3aje.ancija – ne znam samo što ne ideš još dalje – jer avione je valjda trebalo i napraviti , zar ne ?

Objasni mi po čemu si to zaključio pa ću ja posle da objasnim.

Eto opet cepidlačenje – kad sam rekao „jednaki avioni” mislio sam na jednake uslove – zašto da to stalno ponavljam, a ako ćemo
cepidlačiti mogu i ja da kažem da si i ti sad pomenuo „jednakost početnih brzina” koje su jednake nuli pa ni tvoji avioni neće poleteti.

Koji putevi u sistemu vezanom za jedan avion? Znaš li ti šta pričaš? Pa čak i po tebi postoji u tom sistemu samo put onog drugog aviona.
Stalno grešiš. Dokle da te ispravljam?

O tome raspravljamo zato što je problematično – a šalu ili alegoriju ne dozvoljavaš. Dobro, nastojaću da toga ne bude.

Onda ćeš videti samo jednu zvezdu i - nisi dao definiciju tog referentnog sistema jer ne možeš da izbegneš onaj moj pravolinijski.

Pod kretanjem aviona A i odnosu na avion B se podrazumeva kretanje aviona A u sistemu aviona B. Naravno da pilot aviona B može da meri promenu odaljenosti aviona A od njega.



Najzad da priznaš da grešiš. Onda lepo formuliši šta je sve relevantno za relaciju, pa da vidimo.



Pa, ne tvrdi to STR, nego ti. Pogledaj šta si napisao



Znači, to su tvoje dodatne pretpostavke, a ne nešto što je izvedeno iz STR.



Sad smo prešli na etiketiranje. Gde su ti argumenti za to?



Kad budeš naučio diferencijalne jednačine i Košijev uslov, videćeš šta su početni uslovi. Odnose se na stanje celog svemira u jednom trenutku, bez obzira kako se do tog stanja došlo. Kao kada zadaš mase planeta i Sunca i njihove položaje i brzine u jednom trenutku, a onda pustiš zakone da dalje rade svoj posao. Nisam te ja terao da pominješ posledice početnih uslova.



Isto kao da biciklista puca verikalno uvis, pa je hitac u odnosu na njega vertikalan (pašće mu na glavu), a u odnosu na posmatrača sa zemlje kos - klasična mehanika predviđa paraboličnu putanju.



Nisam ti ja kriv što nemaš nijedan izvor sile. To je tvoja fizika. Kao što rekoh, mi relativisti imamo i elisne i mlazne, pa čak i nuklearne motore.



Postoji i put prvog aviona, ako nulu priznaješ kao validnu vrednost. No, poznato je da imaš problema sa nulom.



Pa, opet ne reče što je problematično.



A šta ako je bliža zvezda poluprovidna? Mislim, izvlačiš se.

---

A pešak sa Zemlje mu kaže da laže. (i svi pešaci iz Vasione)

Pa formuliši ti – treba li da prebrojavamo i zube, nokte, prste i ostale detalje koji po tebi anuliraju sličnost ili ti ne znaš
šta je sličnost? Nisi zadovoljan ni sa apsolutnom sličnošću.

Ovo: 0=1 ili kretanje = mirovanje i to sam i koristio u izvođenju protivrečnosti.
Samo sam preneo tvoje misli odnosno tvrdnje.

Ne moje nego tvoje, a ja sam se s njima samo poslužio.

Ja sam, doduše, učio samo deset tipova diferencijalnih jednačina, odnosno rešenja koja zadovoljavaju definisane uslove odnosno
njihove posledice, a što se tiče zakona koji određuju položaje Sunca i planeta tu si tanak ne samo ti nego i čitava dosadašnja nauka.
Seti se samo problema triju tela i ne mlataraj sa onim o čemu nemaš pojma.

Zaboravio si da kažeš „metak” jer on može da padne na glavu i zaboravio si da taj metak ima i brzinu bicikliste.

Sve vi to možda imate, ali mi imamo princip akcije i reakcije, a bez toga su svi vaši motori gomila za otpad. Nisam ni ja tebi kriv što ne znaš
kako se ostvaruje potisak.

Ne ja nego ti! Umesto da priznaš grešku izvlačiš se i to na netačnu foru.

Ja reče ili si zaboravio o čemu raspravljamo.

A ovo kao nije izvlačenje. Gde je definicija?