Nemam i ne zanima me. Kad neko bude okačio oblik koji mogu da pročitam, odgovoriću.
Dakle, neka u stanju manji štapovi imaju sopstvenu dužinu

, a duži štap dužinu
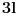
. Neka su u sistemu S vezanom za zemlju koordinate kraćih štapova
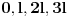
, a dužeg štapa
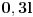
i neka posmatrač trči po zemlji brzinom

u pozitivnom smeru

-ose.
Lorencove transformacije iz sistema S u sistem S' u kome posmatrač miruje glase
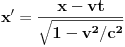
,
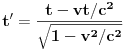
. Kako posmatrač vidi štapove? Izaberimo fiksirani trenutak
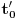
u sistemu S' i razmotrimo tačku P koja je u sistemu S nepokretna i ima prostornu koordinatu

. Izračunajmo njenu prostornu koordinatu u sistemu S' u trenutku kada posmatračev časovnik pokazuje trenutak
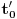
.
Prostorvremenske koordinate tačke P, u trenutku

u sistemu S glase
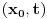
. One u sistemu S' glase
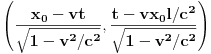
. No, da bismo odredili položaj te tačke za posmatrača u trenutku kada posmatračev časovnik pokazuje vreme
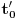
moramo odrediti trenutak

sistema S iz uslova
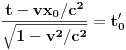
. Dakle,
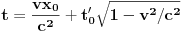
odakle je odgovarajući položaj te tačke za posmatrača u trenutku kada njegov časovnik pokazuje vreme
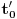
jednak
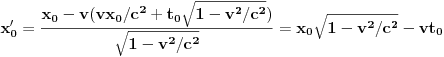
, odakle je jasno da se tačka P kreće u negativnom smeru

-ose brzinom

.
Ako neka tačka miruje u sistemu S u položaju

, ona u sistemu S' ima zakon kretanja
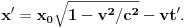
Sad primenite to zamenjujući

sa
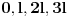
i dobićete zakone kretanja krajeva štapova, kao i kontrakciju njihovih dužina.
EDIT: Ispravih par štamparskih grešaka u poslednjem redu.
[Ovu poruku je menjao Nedeljko dana 16.12.2008. u 14:43 GMT+1]
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.