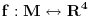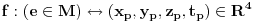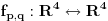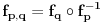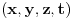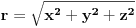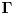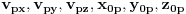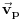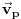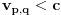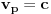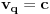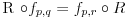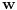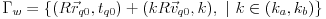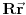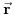Teorija Relativnosti

u nedostatku argumenata
obično se povisi ton ili ( u tvom slučaju ) počinje vrijeđanje.
to je isključivo kada je osoba siromašna duhom

osiječam isto da ti je i taština malo uzela maha u glavi, ali nema veze, to sve govori o tebi.

40cigarettesoncopofcoffie : Skrati ovo (korisničko) ime, da ga mogu napisati. OK, što si mi napisao, ali ima jedan „problemčić“ u onom “sa A. E stanivišta“. I ja sam uporno tragao za „kako“ i „zašto“ dok nisam uočio da to polazno Albert Einstein stanovište nema valjano uporište. Poslije sam tragao zašto je i kako to stanovište moglo proći i zadržati se tako dugo ( tako se izrodila „relativistička algebra“, ljepša, jednostavnija i univerzalnija od svih „matematičkih modela“ vezanih za STR i OTR). Ako je i kod tebe c sa „normalnim sekundama i metrima“ opet c sa „dilatiranim sekundama“ i „kontrahiranim metrima“ onda ne samo da ćeš iskriviti prostor i vrijeme već ćeš iskriviti i matematiku (pa ti „matematički model“ neće štimati u realnom svijetu). Šta misliš o tome zašto je za Ajnštajnovu STR baš potreban (čak nužan) pravougli koordinatni sistem? Zašto se STR ne objašnjava korištenjem polarnog koordinatnog sistema?
Dane, vjera ( i religija) je i korisna i potrebna ljudskom rodu (Ne valjaju mnogi njeni zagovornici, tumači i „branitelji“. Oni su krivi za ...iskrivljivanje istine).
Nego, ono tvoje c je c (za svjetlost) za svakog posmatrača nikako ne mogu da prihvatim drugačije od shvatanja c je c (za zvuk) i njegovu detektabilnost. Da li svojim relativnim kretanjem možemo „ući u oblast detektabilnosi“ ultra ili infra zvuka i čuti ga našim uhom?
“Radi li“ oko za određeno talasno područje isto ono što radi uho za drugo talasno područje?
Pokušajte (važi za sve „posjetioce“) posvetiti pažnju sadržajima koje sugeriše Milan Kecman.

Može biti da sam ja na nekoj od prvih desetak stranica ove teme
napisao:Ja nisam vijernik.Mislio sam pritom na slijepo
vjerovanje tvrđenju nekih "autoriteta" da je to u TR tako i tako.
Vjeruj u to !Nemojte da petljamo religiju u fiziku.Ima za to drugih foruma.
Ja bih radije da nastavimo na trenutku kad je Majklson hrabro objavio
da se njegovi rezultati mjerenja nikako ne slažu sa onim što je računom predvidio.Bilo je tu raznih hipoteza kako to objasniti.Znate li ih?Ja samo znam da je hipoteza koju predlaže Dane bila tada nepoznata.To je stvarno neka novina,originalna,ali ja mislim da nije ispravna.Neki dan sam je testirao kad sam slušao "Radio Šabac".
I nije prošlo.

---

Eh, što mi je zgodno (lako i brzo) diskutovati ovako (http://www.icentar.com/showthread.php?t=314), za ovo je „zaslužan“ McKracken.

Nezgoda je u tome sto ozbiljni relativisti ne uzimaju ucesca u raspravi. Moji argumenti su odavno izlozeni na ovom forumu (ko zna da cita)
Nedostaju kontraargumenti od strane ozbiljnih relativista. Pripite relativiste ne treba shvatati ozbiljno, jer kako od njih ocekivati da shvate
argumente ako celog svog zivota nisu naucili ni svoj materinji jezik (konkretno: ijekavicu)
Milane, objasni mi kako si testirao moju hipotezu, bicu vrlo zahvalan da se eventualno oslobodim moje zablude.
Spreco i oko i uvo rade na istom principu kad je u pitanju frekvencija, samo sto oko detektuje svaki put drugu svetlost.
Ne mogu biti opsirniji jer je moj kompjuter u kvaru. Javljam se od komsije.

vidim da me jedino Sprečo razumije pa se stoga obračam njemu.

uspio sam "blokirati" metar i sekundu u kako ti kažeš „normalne sekunde i metre“
i samo takvi se koriste kroz sve matematičke izvode. da bi sačuvao relativističke pojave uzeo sam
neke druge varijable koje u sebi sadrže relativistički faktor



za galet@world
opet se moram obračati puritancima, čuvarima pravopisa ( mada to nije tema ovog foruma )
http://hr.wikipedia.org/wiki/Hrvatski_pravopis

moje osobno mišljenje je, da je razgovor ( bilo kakav ) projiciranje moje misli u mozak sugovornika,
da li će pritom bit pravopisnih grešaka, griješaka ili grješaka uopće me ne zabrinjava...

Mislim da je lep eksperiment vezan za dilataciju vremena raspad muona.

Ide nesto ovako... muoni nastaju od kosmickog zracenja u gornjim slojevima atmosfere. Brzinu muona koji nam dolaze iz gornje atmosfere moguce je izmeriti pomocu detektora cestica. Ispostavlja se da je bliska brzini svetlosti. Takodje je moguce napraviti spore muone u laboratoriji.

E, ovi spori raspadaju se za tili cas -- toliko brzo da ne bi bilo sanse da oni koji nastanu u gornjim slojevima atmosfere dodju do nas na povrsini Zemlje. Cak i ako idu brzinom svetlosti pravo dole. Medjutim, u detektorima na povrsini moguce je *veoma* lako videti kosmicke muone. Kako to?

Mislim da se ovaj eksperiment radi tokom cetvorogodisnjih studija na gomili univerziteta po svetu.

Naravno, postoji i gomila eksperimenata koji potvrdjuju Doplerov pomak frekvencije svetla. Medjutim, tu moze da se umesa prica o etru i tako-tome... Muoni su nekako bezbedniji za diskusiju :)

Ne veruj -- meri!

Ako si upućen (ili znaš one koji jesu) u prosječno trajanje „života mezona“, korisno bi bilo da otvoriš posebnu temu i vodiš (usmjeravaš diskusiju) posvećenu samo tom pitanju.
Ovako (ad hok) ljubopitljiv sam i interesuje me tvoje mišljenje:
Zašto mezini koji nastaju u atmosferi (na visini 16000m od Zemlje) ne „žive jednako dugo“ (neki se raspadnu brže neki sporije) i ne prelaze jednake puteve?
Ako bi na njihovom putu postavili prepreku (od papira na primjer) da li bi „kraće živjeli“ (od t = 6x10^-5s)?
Da li trajanje „prosječnog života mezona“ zavisi od njihove mase (kolika je?) , energije (kolika je) i materijalne sredine (kolika je prosječna gustina?) kroz koju prodiru (u kojoj izgube energiju brže ili sporije), ili zavisi samo od brzine (kolika je?) njihovog kretanja?
Da li vrijeme raspada zavisi isključivo i samo od brzine njihovog kretanja?
Da li je to uopšte „eksperimentalna potvrda različitog trajanja vremena ili je to potvrda za različito trajanje (postojanje) nečega drugog?
Možeš li pronaći i napisati podatak o srednjoj gustini (količini) materije koju uspiju proći („probiti“) jedni i drugi prije nego što izgube svoju „energiju života“?
Ovdje je upravo pomenut MM eksperiment (još jedna „eksperimentalna potvrda različitog toka vremena“ i „neoboriv dokaz dilatacije vremena“) i kaži svoje mišljenje o proračunu i očekivanom rezultatu (te o zaključcima) u vezi tog „eksperimenta“. Šta misliš, koliki je broj onih koji su provjeravali proračun, a koliki je broj onih koji su vjerovali proračunu?
Vida Žigman: „STR je teorija sa neoborivom i mnogostranom eksperimentalnom verifikacijom“.
Ti citiraš: „Ne veruj – meri“! Da li si razmišljao šta (i kako) „meriš“, a šta i kako zaključuješ u vezi tog mjerenja (na primjer u konkretnom eksperimentu koji pominješ)?!
Ne vjeruj – provjeravaj!

mioni... http://doc.cern.ch//archive/el...neric/public/cer-002599796.pdf

---

Vida Žigman: „Specijalna teorija relativnosti“, strana 35. 2.4 Realni eksperimenti
“......Među česticama koje se izučavaju u fizici visokih energija postoje naelektrisane čestice π-mezoni (pioni), pozitivne (π⁺) i negativne (π^-), sa masom između mase elektrona i mase protona. Pioni nastaju bombardovanjem akceleratorske mete visokoenergetskim protonima pri čemu π-mezoni napuštaju metu brzinom vrlo bliskom c. Poznato je da su pioni nestabilni i da je vreme njihovog poluživota u stanju mirovanja 1,77x10^-8s.......“
Cibernoid, (zamisli da ti pitanja postavlja neko blizak i drag, te mu u tom smislu odgovori)
1. Da li se ova („vrlo bliska c“, v ≈ 2,97x10⁸m/s) brzina izračunava (kako) ili mjeri (kako)?
2. Je li definicija metra i sekunde u toj brzini v u skladu sa SI i klasičnom fizikom?
3. Postoje li pioni u stanju mirovanja?
4. Da li je ovo vrijeme njihovog poluživota u stanju mirovanja 1,77x10^-8s eksperimentalno utvrđeno (kako) ili izračunato (kako)?

Odgovor DaniNemam ja namjeru da namećem svoje mišljenje ostalima.
Dane ima svoju teoriju i buni se što je kritikujem.Ja nemam svoju teoriju.
Evo priče o radio Šapcu:
Kada ja vrtim dugme tražeći radio Šabac,osjetim da je ispočetka slabašak prijem.
Kasnije je sve jači I onda počinje slabiti.Nađem sredinu.
Ja sam zapravio tražio najbolju frekvenciju mog radija,kako bi bila razonantna= ista
kao I radio Šabac.Ali izgleda da ni Šabac ne emituje strogo na jednoj frekvenciji.
Oko one centralne najjače,u okolišu ima zagađeno još ponešto.To je zakonom (društvenim) dozvoljeno do neke granice.
Svjetlost I radio emisija imaju isti el. magnetni karakter.
Slažem se ja sa Danom da emiter šalje svjetlost različitim brzinama.Što veća temperatura to širi dijapazon brzina.Ali šta kaže doplerov efekat?
-----------------------
Emiter bi trebao imati neki spektar brzina.Od c-v(max) do c+v(max).Intenzitet kod c je najveći.A lijevo i desno intenzitet slabi polako do nule.Ako dođe do relativnog kretanja emitera I prijemnika,trebalo bi da slabi intenzitet?Čak pri nekim brzinama većim od v(max)bi nestalo prijema.Ali ne slabi!Doplerovim pomakom ne
opada snaga el.magnetnih talasa.To je utvrđeno.Kada ja jurim biciklom k Šapcu ili nazad
samo moram malo popraviti frekvenciju na niže /više,a jačinu omiljene pop folk muzike ne mijenjam.
Vjerujte mi,a ko ne vjeruje neka proba.

---

zna li neko za besplatan pristup
izvorno publiciranim znanstvenim radovima i eksperimentima, preko neta ?
( znam da ga imaju svi profesori, ali da ih netlačim "on daily bases" )

Odavde imam pristup vecini casopisa ali je restriktovan pristup po IP adresi. Mislim tj. prilicno sam siguran da ne moze da se nadje besplatno -- moraces uvek da cimas nekog sa institucije koja ima pristup. Ako spomenemo neke radove ovde na diskusiji, mogu da ih prosledim, ne znam samo da li na forum (opet copyright) ili na licni mail.

Cybernoid -- divan clanak. Pogotovo posto mislim da je CERN merenje bolji rezultat od merenja atmosferskog vremena poluraspada koje sam ja naveo. Naime, u akceleratoru u kojem cirkulisu muoni u CERN eksperimentu vlada visoki vakuum (p<1e-11 atm => gustina 10^11 puta manja od gustine vazduha) i sudari muona sa materijom su stoga zanemarljivi. Argument za zanemarivanje sudara sa materijom u akceleratoru je sledeci:

Siguran sam da se lako mogu naci merenja vremena poluraspada muona u:
a) vazduhu
b) vodi (elektroni + vodonik + kiseonik)

Takodje sam siguran da ce vreme poluraspada u vodi biti mnogo krace. Posto voda ima znatno vecu gustinu od vazduha, razlika u izmerenom poluvremenu raspada bila bi cisto do interakcije sa elektronima/vodonikom/kiseonikom ILI do smanjenja brzine muona u vodi. Slucaj b) vec vodi na zavisnost vremena poluraspada od kretanja -- stav koji Spreco hoce da pobije. Zbog toga, ako ne verujemo u dilataciju vremena, onda bi *sigurno* morali da interpretiramo smanjen zivot muona u vodi kao nesto sto potice od elektrona + vodonika + kiseonika (vodonik + elektroni i kiseonik su glavni kontaminanti u vakuumskim high-power RF sistemima) I to nesto bi bilo reda velicine t = nekoliko ns. E, posto je CERN vakuum 10^13 puta redji od vode, to znaci da t_raspada_od_materije > 1s sto je zanemarljivo sporo u odnosu na merenja iz clanka.

Dakle, za potrebe eksperimenta, akcelerator izuzima ostalu materiju iz problema -- toliko sto se Sprecine kritike vezane za mogucu interakciju sa vazduhom/papirom tice. Jedino sto ostaje je uticaj magnetnog polja akceleratora. To moze biti problem.... ali, zanemaricu ga za sada.

Sto se brzine muona pri merenju tice, to clanak nije specificirao. Medjutim, prilicno sam siguran da su CERN istrazivaci i to prilicno direktno izmerili. Mislim, nesto u stilu:
a) ukljuci injekcioni zrak muona u akcelerator
b) gledaj kada se pojavi prvi signal naelektrisanih cestica 500m niz akcelerator

Razlog sto ne navode broj je najverovatnije to sto ta brzina ispadne bliska c. Posto oni veruju u STR, umesto brzine navode relativisticki impuls koji je relevantna brzina za skretanje i navodjenje cestica magnetnim poljem akceleratora: 1.274GeV/c. Uz masu muona sa CODATA internacionalne baze fizickih velicina:
muon mass 1.883 531 40e-28 +- 0.000 000 33e-28 kg
iliti
muon mass energy equivalent in MeV 105.658 3692 +- 0.000 0094 MeV
+ STR dobijamo v = c - 10^6 m/s. Kao sto rekoh, prakticno c.

Pri toj brzini muona, oni *direktnim* merenjem struje u akceleratoru dobijaju (26.15+-0.03)us.

E, sad, pitanjem da li je neko izmerio raspad muona u mirovanju, Spreco me je malo zeznuo -- bas je u pravu sto je sumnjicav.
Jer, bio sam siguran da, posto se muoni tako cesto navode kao primer za STR, neko je to direktno izmerio. Mislim, nesto u stilu -- uhvatis 1e3 muona u RF zamku za naelektrisane cestice pa meris kako ti nestaju. Nazalost, vreme poluraspada muona navedeno u referenci 8 (Feinberg and Lederman, Ann. Rev. Nucl. Sci. 13, 466 (1968)) je samo 2.2us. Nema bas puno vremena za hvatanje!
Stoga, nacin na koji reference iz reference 8 kao i novija merenja hvataju mirujuce muone je tako sto ih sudare sa jezgrima vodonika/helijuma u meti akceleratora pa onda mere vremensku raspodelu sekundarnih proizvoda raspada pomocu detektora koji okruzuju metu. U tom slucaju Spreco 100% ima pravo da pita o uticaju materije!

Nadam se da neko moze da nadje merenja slicna gorenavedenim pri drugim impulsima muona. U tom slucaju, zakljucili bi da vreme poluraspada muona *za muone koji se brzo krecu* zavisi *nekako* od brzine kretanja. U tom slucaju, bez dilatacije vremena,
Kako vreme poluraspada *necega* moze da zavisi od brzine njegovog kretanja *u praznom prostoru*? Jer, cime ces da meris vreme necega sto se krece? Nuklearni raspad bi bila dobra ideja.... ono, kao radionucleotide dating :)

Bez ovakvih merenja, Sprecin komentar o uticaju materije ostaje validna kritika.

Napomena -- u mojoj poruci i u Cybernoid-ovoj poruci radi se o muonima a ne o pi-mezonima. Uprkos tome, upravo sam na netu -- http://math.ucr.edu/home/baez/...iments.html#round-trip%20tests
video da su radjena merenja i sa pionima veoma slicna merenjima sa muonima. U svakom slucaju, muoni i pioni jesu *veoma* razlicite cestice (muoni su leptoni i interaguju elektroslabo a pioni mezoni koji interaguju i jako).

Svaki dan covek nauci nesto novo :))

Povodom vremena poluraspada muona u materijalnoj sredini:

Vec sam spomenuo da je ovo merenje cesta laboratorija na univerzitetima. Primer je:
www.pma.caltech.edu/~ph77/labs/exp15.pdf

Naravno, profani nece da daju rezultate studentima. Write-up nekih studenata sa drugog univerziteta mozete da nadjete ovde:
mxp.physics.umn.edu/s01/Projects/Muon/muonfinal1c.pdf (2.1us vreme poluraspada u izvesnoj vrsti providne plastike)

Dakle:
tau = 26.15us pri impulsu 1.274GeV/c odnosno brzini bliskoj c, u vakuumu
tau = 2.2us za muone isudarane/zaustavljene u meti od tecnog vodonika
tau = 2.1us za muone u plastici izmerili neki studenti

Trazi se: tau pri manjim impulsima/brzinama u vakuumu i/ili ubedljiv argument zasto materija ne skracuje dramaticno vreme poluraspada u raznim metama (CERN, scintillator plastika, TRIUMF, etc.)

Prvo da se izvinim svima na forumu ako monopolizujem prostor muonima i uopste fizikom brzih cestica. Pokusacu da se nadovezem direktno na STR/MM diskusiju.

Prvo da odgovorim na par Sprecinih pitanja:
1. Da li se ova („vrlo bliska c“, v ≈ 2,97x108m/s) brzina izračunava (kako) ili mjeri (kako)?
Brzina se meri na taj nacin sto se oko mete u kojoj se proizvode pioni/muoni/whatever nalaze raznorazni detektori. Rastojanje svakog dela tih detektora od mete je tacno izmereno nekom vidom metra kalibrisanom prema SI standardu. Kada pioni/muoni/whatever prodju kroz detektore, detektori kazu "klik". Taj klik onda brzo ide u diskriminator koji odmah zapise trenutak kada je klik dosao u odnosu na takt referentnog casovnika.
Svaka cestica prodje kroz nekoliko detektora i ponekad napravi nekoliko klikova. Kada se to desi, zna se rastojanje izmedju prostornih tacaka u kojima su se desili klikovi kao i vremenski interval izmedju klikova. Stoga se zna i brzina cestice od jednog do drugog klika.

2. Je li definicija metra i sekunde u toj brzini v u skladu sa SI i klasičnom fizikom?
Kao sto sam rekao, dimenzije delova detektora se mere nekim vidom metra (mernog instrumenta) kalibrisanog prema SI standardu. Referentni casovnik je medjutim sinhronizovan je direktno sa primarnim casovnikom citavog eskperimenta koji se bazira na Cs atomskom standardu koji je pak *primarna* SI definicija sekunde. Dakle, i metar i sekunda su povezani sa fizickim SI standardima.

3. Postoje li pioni u stanju mirovanja?
S obzirom na moju muku sa muonima iz prethodnog komentara, odgovor je najverovatnije: samo isudarani/iztermalizovani sa jezgrima i atomima mete. Dakle, za sada ne postoje u vakuumu :(

4. Da li je ovo vrijeme njihovog poluživota u stanju mirovanja 1,77x10-8s eksperimentalno utvrđeno (kako) ili izračunato (kako)?
Mete, mete, proklete mete.... Da li sam vec rekao "proklete mete"? :)

5. Misljenje o MM?
Pobija etar. Dok Zemlja ide oko Sunca, pola godine eksperiment ide na jednu stranu a pola na drugu stranu u odnosu na Sunce. Ako se svetlost prostire kroz *nesto* (etar) koje se krece nekom const brzinom u odnosu na Sunce, brzina eksperimenta u odnosu na to *nesto* (etar) bice promenjljiva tokom godine. Medjutim, rezultat eksperimenta *ne varira* tokom godine. Dakle, ne postoji klasican medijum u kroz koji se svetlo prostire tj. u odnosu na koji Maxwell prica o brzini svetlosnih talasa.

U odnosu na sta onda Maxwell predvidja brzinu svetla? Odgovor se namece: u odnosu na -- nista -- *svi* inercijalni posmatraci za koje vazi ista klasicna fizika bi trebali da mere istu brzinu!

Dalji komentar o MM (kontrakcija duzina, dilatacija vremena, etc.): Bez daljeg razmisljanja -- nista. Rezultat stoji. Sada ga, kao fizicari i skeptici prema STR trebamo sami objasniti... kao i druge eksperimentalne rezultate koje moramo kriticki da posmatramo.
Ako sumnjate u metodologiju MM *kao testa za etar*, i to bi bila odlicna tema.

Pitanje za Sprecu:

Kazes da se slazes sa konstantnosti brzine svetlosti u homogenoj sredini. Da li pod tim podrazumevas sledece:
"
U tacku A stavim sijalicu. Onda uzmem metar i uglomer i napravim 1m x 1m x 1m pravougaonu "koordinatnu" resetku sa jednim temenom u tacki A. U svaku tacku resetke stavim casovnik. Sve casovnike sinhronisem na neki klasican razuman nacin (ovo mi sve puno zvuci kao onaj detektor cestica sa svojim metrom i atomskim casovnikom :) ). Na brzinu ukljucim i iskljucim sijalicu. Merim kada impuls svetla dodje do svakog od casovnika.
Zakljucim da je u svim delovima prostora brzina svetlosti ista tj. da je brzina svetlosti u homogenom prostoru homogena.
"?
Da li se *ne* slazes sa sledecim:
"
Ja se sa svim mojim metrima, casovnicima, etc., krecem u odnosu na sijalicu. U nekom trenutku sijalica se ukljuci i iskljuci. Merim kako se rezultujuci svetlosni impuls pogodi svaki od mojih casovnika. Na taj nacin izracunam brzinu svetlosnog fronta iz sijalice.
Dobicu 299 792 458 m/s.
"

Bitan komentar za tekuce i buduce diskusije, ukoliko ga neko vec nije naveo:

Trenutna SI definicija metra:
Metar je rastojanje koje svetlost predje u vakuumu tokom vremenskog intervala od 1/299 792 458 sekunde.
Dakle, u trenutnom SI sistemu brzina svetlosti je matematicka konstanta!

Trenutna SI definicija sekunde:
Sekunda je trajanje 9 192 631 770 perioda radijacije koja odgovara tranziciji izmedju dva hiperfina nivoa cesium 133 atoma.

Trenutna SI definicija kilograma:
Glupava cigla u Parizu. Medjutim, veci stepen reproducibilnosti i preciznosti u merenju i poredjenju masa elementarnih cestica moguca je ako se za definiciju jedinice mase koristi recimo masa elektrona u mirovanju. Elektroni se danas redovno hvataju i hlade do prakticno apsolutnog mirovanja (google: Electron Penning Trap + Gabrielse + Harvard). Takodje je moguce fantasticno precizno porediti njihovu masu sa masama jona/jezgara (google: Thompson + Penning Trap)

Palo mi je jos nesto na pamet vezano za cisto logicku strukturu STR. Prilicno sam siguran da su sledeci cisto matematicki postulati dovoljni za izvodjenje citave i kompletne kinematike (ono, bez energije, impulsa, sila, E=mc^2 -- samo kretanje slobodnih tela posmatrano od strane drugih slobodnih tela pomocu metara i casovnika) STR.

Stvar je manje-vise ono standardno: "c je ista i konstantna za sve inercijalne posmatrace u svim pravcima"...

Aksiom 1 -- Postojanje prostor-vremena kao matematicke visestrukosti

Za svakog inercijalnog posmatraca postoji matematicka identifikacija (bijekcija) skupa svih fizickih dogadjaja sa cetvorkama realnih brojeva (prostor-vreme koordinate dogadjaja u odnosu na ):

.

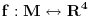
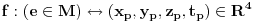
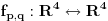
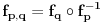
Za svaka dva inercijalna posmatraca i , bijekcija definisana sa je diferencijabilna. Ova funkcija odgovara prelasku iz opisa prostor-vremena sa stanovista koordinata posmatraca na koordinate posmatraca

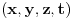
Notacija: Cetvorke koordinata pisacu cesto kao gde je i

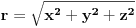
Definicija 1 -- Ravnomerno kretanje:

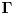
Skup dogadjaja definisan sa:

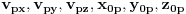
pri cemu su i realni brojevi nazivamo trajektorijom objekta koji se u odnosu na posmatraca krece ravnomerno brzinom .

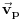
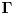
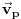
Fizicki govoreci, je prava linija na prostor-vreme dijagramu posmatraca koja odgovara brzini kretanja u odnosu na .

Aksiom 2 -- ravnomerno kretanje inercijalnih posmatraca
Za svakog inercijalnog posmatraca , skup tacaka u prostor vremenu kroz koje prolazi bilo koji drugi inercijalni posmatrac odgovara trajektoriji objektra koji se u odnosu na krece ravnomerno izvesnom brzinom

Aksiom 3 -- konacnost brzine inercijalnih posmatraca
Postoji pozitivan realan broj takav da za svaka dva inercijalna posmatraca i ,

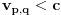
Aksiom 3 -- konstantnost brzine svetlosti za sve inercijalne posmatrace
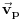
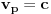
Za svaka dva posmatraca i , ako se objekat X krece u odnosu na posmatraca ravnomerno brzinom takvom da je , X ce se takodje kretati ravnomerno u odnosu na brzinom takvom da je .

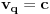
Aksiom 4 -- izotropnost prostor-vremena (suvoparna matematicka formulacija)
Za svaku 3D rotaciju i svaka dva inercijalna posmatraca i ,

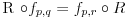
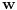
Gde je inercijalni posmatrac cija je trajektorija u odnosu na opisana sa

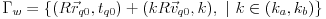
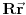
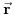
gde prestavlja rotaciju vektora pomocu .
Intuitivno, ovo kaze da ako razmotris STR pod nekim okolnostima, a onda okrenes glavu svim inercijalnim posmatracima na neki (relativno u odnosu na njihov originalni polozaj glave) isti nacin, STR ce izgledati isto.

Ako su ovo dovoljni aksiomi (sto mislim da jeste slucaj), onda poricanje STR => (cisto matematicki/logicki)
poricanje izotropnosti praznog svemira ili
poricanje konstantnosti brzine svetlosti za sve inercione posmatrace ili
poricanje brzine svetlosti kao gornje granice brzina inercionih posmatraca tj. slobodnih tela ili
poricanje ravnomernog kretanja inercionih posmatraca merenih koordinatama (lenjirima i casovnicima iz prehodnih poruka) drugih inercionih posmatraca ili
poricanje mogucnosti unikatnog opisa dogadjaja u prostor-vremenu pomocu 4 realne koordinate od strane inercionih posmatraca

Ovo sam nekako morao da napisem jer sam puno puta video izvodjenja Lorentz-a sa komentarima tipa: "a naravno, svemir je homogen"; "a naravno, ako idemo brzinom -v u pravcu x, transformacija u t,y i z je ista i kada idemo brzinom +v u pravcu x (to bi bila refleksija a ne rotacija!)", itd. Malo vise ide na zivce, pogotovo u poredjenju sa veoma preciznom postavkom OTR.

Marko

P.S.
Dobra referenca: Taylor and Wheeler, Spacetime Physics -- skoro nema ni jedne formule a o svemu prica.

<sub>[Ovu poruku je menjao mcetina2 dana 16.12.2006. u 12:49 GMT+1]

[Ovu poruku je menjao mcetina2 dana 16.12.2006. u 12:51 GMT+1]</sub>

Marko, hvala na opširnom sadržaju i tonu odgovora (mnogo je prijatniji „saradnički“ od „svađalačkog“ tona).
Dr. Vida Žigman, odmah nakon piona opisuje i mione, ali u oba primjera protura (površnom čitaocu) poluistine kao čvrste i neoborive eksperimentalne dokaze postavki STR. Ivan Supek koristi i jedne i druge u svom izvođenju eksperimentalnih potvrda postavki STR. Cibernoid je i plasirao link kao svoj doprinos „neoborivim eksperimentalnim dokazima“ ispravnosti postavki STR.
Ovako kako je tekst formulisala Vida Žigman, površan čitalac (većina studenata) neće obratiti pažnju da se u eksperimentu sa pionima stvarno i jedino eksperimentalno mjeri samo „vrijeme koincidencije“ t i dužina puta d, a sve ostalo izračunava, pa i brzina v = d/t , (svojevremeno sam se pitao: da li je stvarno kretanje piona na ovom putu u olovu konstantno ili jednako promjenljivo, šta bi se promijenilo kada bi olovo bilo „pokretno“, itd).
Brojke koje je su ubačene u navedenom udžbeniku su očito „uštimovani podaci“ ( t = 1,3x10^-7s , v = 2,97x10⁸m/s i d = 39m). Ovakvim uštimovanim podacima studenti vjeruju i kasnije (kao profesori fizike, kao pravi vjernici) tvrdoglavo ih brane i dalje šire kao „neoboriv dokaz“ u prilog STR. Površan čitalac će vjerovati da su svi podaci i brojke eksperimentalno utvrđeni i „naučno utvrđeni“.
U udžbeniku Vide Žigman (strana 37.) posebno me „naljutila“ ovakva rečenica (izjava):
“Drugim rečima, jasno je da se razlika u merenju rastojanja od 39m i 5,3m ne može uvrstiti ni u kakvu „grešku“ merenja“. Ovako formulisana rečenica sugeriše (nameće) zaključak da je u istom eksperimentu (dakle u eksperimentu sa pionima) stvarno, objektivno i realno izmjereno i 39 m i 5,3m. Pa, zar ovakve formulacije ne zaslužuju (demokratski, objektivno i realno) „deset po turu“?!
Za MM eksperiment ( više na: (http://www.icentar.com/showthread.php?t=314), vidjeti Matematika – „Relativistička algebra“ i STR „Ajnštajnov voz u 7 slika“) iznosim tvrdnje (izjave):
Proračun razlike optičkih puteva u MM interferometru ct – 2ct'
1. a) nedopustivo – pogrešno izračunata veličina razlike;
b) ne zavisi od smjera kretanja Zemlje;
c) ne zavisi od „mnogobrojnih refleksija svjetlosti“ unutar interferometra;
d) ne zavisi od zakretanja krakova interferometra za 90°, te je
2. a) „očekivani rezultat“ eksperimenta pogrešno utvrđen,
b) „očekivani rezultat“ eksperiment nije potvrdio,
c) ni jedan detalj, niti bilo koja veličina u MM eksperimentu nije suprotna „klasičnoj fizici“ i Euklidovoj geometriji.

- Izotropnost praznog svemira – ne sporna ( u smislu Euklidove geometrije);
- Konstantnost brzine svjetlosti u „izotropnom praznom prostoru“ – da (ne ovisna od svega ostalog: kretanja izvora, kretanja posmatrača, ...i njihovih relativnih mehaničkih kretanja, inercijalnih ili ne inercijalnih sasvim je ne bitno); brzina i pravac prostiranja svjetlosti se mijenja u zavisnosti od prisustva i strukture materije u tom prostoru.
Konstantnost brzine svjetlosti u „izotropnom praznom svemiru“ obezbjeđuje sljedeću fizičku realnost: Ako je posmatrač u sredini pokretnog osječka AB pravca po kojem se kreće posmatrač konstantnom brzinom 0 < v < c , i ako posmatrač šalje svjetlosni signal u prostor oko sebe onda će se svjetlost prostirati brzinom c u svim pravcima i smjerovim u odnosu na tačku P i za vrijeme t obrazovati sferu oko tačke P poluprečnika r = ct. Za to vrijeme posmatrač će se pomjeriti za dužinu SS' = vt, tačka B će se pomjeriti za dužinu BB' = vt, tačka A će se pomjeriti za dužinu AA' = vt, svjetlost koja je krenula iz P susrest će prije tačku A (koja dolazi u susret svjetlosnoj zraki c+v ), nego što će stići u tačku B (koja bježi ispred svjetlosne zrake c-v). Ovakav opis dao je Ajnštajnov saradnik L. Infeld, a isti takav opis dao je A. Ajnštajn sa opisom dva istovremena udara munja u tačkama A i B. Šta to implicira? Da ne funkcioniše tumačenje „postulata 2.“ o širenju svjetlosti i u odnosu na „pokretnog posmatrača“ brzinom c u svim pravcima i smjerovima.
- poricanje brzine svjetlosti kao gornje granice brzina slobodnih tijela , za sada nema osnova u realnom svijetu (zbog pretvaranja - transformacije materije u plazmu, za koju važe drugačiji fizički zakoni), ali matematičko tretiranje po Ajnštajnovim i Lorencovim formulama dozvoljava sasvim ravnopravno korištenje brzina 0 < v < c < ∞ , bilo kojih skalarnih vrijednosti (što nam tako lijepo omogućava sagledavanje logike Ajnštajnovih i Lorencovih formula i postavki ako ih tretiramo sa , na primjer , c = 100m/s i v teži c).
- Ako za opis nekog fizičkog zbivanja nisu ravnopravni svi matematički modeli onda treba prvo posumnjati u opis fizičkog zbivanja koje zahtijeva: baš pravougli koordinatni sistem, posebne jedinice za svaki sistem, promjenu dosadašnjih shvatanja i prostora i vremena i ... još mnogo toga.
- poricanje unikatnog opisa događaja u prostor-vremenu pomoću 4 realne koordinate nije ni potrebno ni nužno, jer uvijek možemo tretirati kretanje nekog volumena (prostora ispunjenog ili praznog sasvim je sve jedno) kao cjeline.
E, ima toga još mnogo , mnogo više za kazati ( u osporavanju STR Alberta Ajnštajna).

sobzirom da se trudimo podignuti kvalitetu
ovog foruma, prijesvega na dobrobit nas samih koji sudijelujemo u njoj aktivno
zamolio bih da pišete ( barem u zagradi )
ispravno imena poznatih znanstvenika koje spominjete

- npr. najčešča greška je Lorenc:

•Hendrik Antoon Lorentz
Lorentzova transformacija


•E. Lorenz
Lorenz je otkrio ono što će kasnije postati poznato kao “učinak leptira”