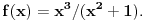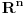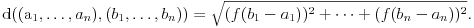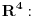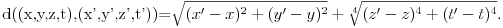Srodne teme
Navigacija
Lista poslednjih: 16, 32, 64, 128 poruka.

Teorija Relativnosti

elitemadzone.org :: MadZone :: Teorija Relativnosti
(Zaključana tema (lock), by Tyler Durden)
Strane: < .. 1 2 3 4 5 6 7 8 9 ... Dalje > >>

[ Pregleda: 475787 | Odgovora: 2583 ] > FB > Twit

Postavi temu

Autor
Pretraga teme: Traži
Markiranje Štampanje RSS

Cybernoid II

Član broj: 14852
Poruke: 528

Sajt: www.youtube.com/watch?v=7..


+1 Profil

icon Re: Teorija Relativnosti25.07.2004. u 06:28 - pre 253 meseci
Citat:
dva broda, četiri posmatrača,relativna brzina mjerena svjetlosnim signalima. Ako jedan posmatrač može imati izbor:1. smatrati da miruje i on i njegov brod; 2. smatrati da se kreće i on i njegov brod - zašto je to "zabranjeno" njihovim dvojnicima?). Sve je i fizički i logički izvodivo i ostvarivo.


Zaboravio si samo dve sitnice:
princip rada atomskog casovnika i laserskog daljinometra, na kojima se zasnivaju definicije metra i sekunde.

posmatrac 2 koji "misli" da se krece vreme i razdaljinu ne meri u sekundama i metrima, nego u nekim pomesanim jedinicama. Ako preracuna velicine u sekunde odnosno metre docice do istih rezultata i zakljucaka kao i posmatrac 1 koji "misli" da miruje.

Pokusaj da shvatis razliku izmedju koordinata i duzina, apstraktnih velicina i fizickih velicina u konkretnim jedinicama mere, promenljive i invarijante.

Kako 5Kg "pretvoriti" u 20Kg? Nista lakse. Zamisli da ti na pijaci prodaju lubenice. Vesti seljak stavi palac na vagu i lubenicu od 5Kg ti proda kao lubenicu od 20Kg.
Time se nece povecati broj semenki u lubenici.

Kako 5eura pretvoriti u 20eura? Nista lakse zamenis eure u dolare i objavis devalvaciju eura pa dolare vratis u eure. Naravno kupavna moc te kolicine novca ostaje ista.
#!/usr/bin/basho
mv frog ancient_pond
echo "Splash!"
 
0

srki
Srdjan Mitrovic
Auckland, N.Z.

Član broj: 2237
Poruke: 3654
*.dialup.xtra.co.nz



+3 Profil

icon Re: Teorija Relativnosti25.07.2004. u 07:06 - pre 253 meseci
Citat:
Sprečo: Pa ako imamo samo dva tijela nema se tu navoditi šta u odnosu na šta. Imaš K' i K, pa biraj koji se kreće u odnosu na onaj drugi.


Pa ako je tako onda je rezultat isti. Nema to veze da li ti smatras da se tvoj sopstveni koordinatni sistem krece prema drugom ili se taj krece prema tvom. U principu i jedno i drugo je tacno. Znaci isti rezultat bi dobili.
 
0

Nedeljko
Nedeljko Stefanović

Nedeljko
Član broj: 314
Poruke: 8706
*.dial.InfoSky.Net



+2802 Profil

icon Re: Teorija Relativnosti25.07.2004. u 10:13 - pre 253 meseci
Citat:
Cybernoid II: Zaboravio si samo dve sitnice:
princip rada atomskog casovnika i laserskog daljinometra, na kojima se zasnivaju definicije metra i sekunde..


Definicija sekunde jeste atomska, ali atomski časovnik nije zasnovan na toj definiciji, već na periodu radioaktivnog poluraspada nekog gasa i statističkoj proceni broja raspalih čestica u jedinici vremena. Sekunda je zapravo određen broj prelazaka elektrona sa neke orbite u neku drugu kod nekog atoma.

Citat:
Cybernoid II: 
posmatrac 2 koji "misli" da se krece vreme i razdaljinu ne meri u sekundama i metrima, nego u nekim pomesanim jedinicama. Ako preracuna velicine u sekunde odnosno metre docice do istih rezultata i zakljucaka kao i posmatrac 1 koji "misli" da miruje..


Ne, obojica mere dužinu i vreme u metrima i sekundama, samo što njihovi daljinometri i časovnici daju različite vrednosti. Da li si čuo za Mesbauerov efekat? Kada zagreješ radioaktivni preparat tako da prosečna brzina atoma preparata bude relativistička, onda ćeš izmeriti "plavi pomak" u spektru zračenja koje meriš. To je zato što atomi emituju zračenje odgovarajuće talasne dužine iz svoje tačke posmatranja, ali se ti krećeš u odnosu na njih, pa vidiš kraće talasne dužine.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
 
0

Nedeljko
Nedeljko Stefanović

Nedeljko
Član broj: 314
Poruke: 8706
*.dial.InfoSky.Net



+2802 Profil

icon Re: Teorija Relativnosti25.07.2004. u 10:21 - pre 253 meseci
Citat:
Sprečo:volio sam da ste koristili "izmjerenu dužinu" ct = c 20g = x. Želio sam iskoristiti Vaš konkretan proračun kao oslonac za "nešto novo - što nećete naći u udžbenicima". Želim na tom konkretnom primjeru iskazati razliku između Ajnštajnovog t' i Lorencovog x'/c = t'.


Pa ako se astronaut kreće brzinom od 0,8c, onda onaj put koji on prevali za 20 godina svetlost prevali za 20*0,8=16 godina. Opet se dolazi do istog rezultata.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
 
0

Cybernoid II

Član broj: 14852
Poruke: 528

Sajt: www.youtube.com/watch?v=7..


+1 Profil

icon Re: Teorija Relativnosti25.07.2004. u 10:45 - pre 253 meseci
Sto se tice Mesbauerovog efekta on je posledica temperature.
Citat:
Considering that a very precise definition of the unit of time is indispensable for the International System, the 13th CGPM (1967) decided to replace the definition of the second by the following (affirmed by the CIPM in 1997 that this definition refers to a cesium atom in its ground state at a temperature of 0 K):

The second is the duration of 9 192 631 770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the cesium 133 atom.


Citat:
Sekunda je zapravo određen broj prelazaka elektrona sa neke orbite u neku drugu kod nekog atoma

...u stacionarnom koordinatnom sistemu, vezanom za posmatrani atom, u kome su jedinicni koordinatni vektori u pravcu vremenske i prostorne koordinatne ose medjusobno ortogonalni duz putanje posmatranog atoma.

Drugim recima, u ravnom prostoru talasna jednacina ima kanonicki hiperbolicni oblik u inercijalnom koordinatnom sistemu.

Citat:
Ne, obojica mere dužinu i vreme u metrima i sekundama


Ne, posmatrac 2 koji "misli" da se krece koristi Galilejeve transformacije iz inercijalnog u neinercijalni koordinatni sistem t'=t x'=x-vt. U tom slucaju jedinicni koordinatni vektori u pravcu vremenske i prostorne koordinatne ose nisu medjusobno ortogonalni.


#!/usr/bin/basho
mv frog ancient_pond
echo "Splash!"
 
0

Cybernoid II

Član broj: 14852
Poruke: 528

Sajt: www.youtube.com/watch?v=7..


+1 Profil

icon Re: Teorija Relativnosti25.07.2004. u 12:21 - pre 253 meseci
Ovde su nabrojane neke istine o relativnosti, proverene brojnim eksperimentima.
http://www.physics.gmu.edu/cla...tr103/CourseNotes/rlt_splr.htm
Oni nisu u suprotnosti sa zdravim razumom, vec sa dodatnim zabludama nasledjenim iz klasicne fizike.
#!/usr/bin/basho
mv frog ancient_pond
echo "Splash!"
 
0

Nedeljko
Nedeljko Stefanović

Nedeljko
Član broj: 314
Poruke: 8706
*.dial.InfoSky.Net



+2802 Profil

icon Re: Teorija Relativnosti25.07.2004. u 15:08 - pre 253 meseci
Citat:
Cybernoid II: Sto se tice Mesbauerovog efekta on je posledica temperature.

A šta je temperatura nego kretanje čestica tog preparata?
Citat:
Cybernoid II: Ne, posmatrac 2 koji "misli" da se krece koristi Galilejeve transformacije iz inercijalnog u neinercijalni koordinatni sistem t'=t x'=x-vt. U tom slucaju jedinicni koordinatni vektori u pravcu vremenske i prostorne koordinatne ose nisu medjusobno ortogonalni.

Ne. On ne koristi nikakve transformacije (pogotovu ne Galilejeve), već
merne instrumente. Recimo, laserski daljinomer i atomski časovnik. Ako imamo voz i peron koji su iste dužine i ako u lokomotivi sedi mašinovođa, a na peronu putnik, onda će prilikom njihovog uzajamnog kretanja putniku voz da izgleda kraći od perona, a mašinovođi peron kraći od voza. Pritom je dovoljno da koriste oči, bez obzira da li znaju Galilejeve ili bilo koje druge transformacije

Sa druge strane, ako peron i voz u stanju mirovanja imaju istu širinu, onda će prilikom prolaska voza pored perona i putnik i mašinovođa videti da peron i voz i dalje imaju istu širinu. Neko će reći da naše oći toliko brze promene ne mogu da registruju, kao i da nemamo toliko brze vozove, ali zato isti eksperiment možemo obaviti sa radioaktivnim preparatom. To je suština Mesbauerovog eksperimenta.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
 
0

Cybernoid II

Član broj: 14852
Poruke: 528

Sajt: www.youtube.com/watch?v=7..


+1 Profil

icon Re: Teorija Relativnosti25.07.2004. u 16:23 - pre 253 meseci
Citat:
Ne. On ne koristi nikakve transformacije (pogotovu ne Galilejeve), već
merne instrumente. Recimo, laserski daljinomer i atomski časovnik...Pritom je dovoljno da koriste oči, bez obzira da li znaju Galilejeve ili bilo koje druge transformacije


sta koristi oci ili instrumente?

On misli da se krece brzinom v, dakle po njemu njegove prostorne koordinate (njegove trajektorije) xo se menjaju, odnosno izvoriste njegovog koordinatnog sistema je vezano za neki drugi (referentni) objekat za koji on misli da miruje, dok sat sa koga ocitava vreme t drzi u ruci. Polozaj nekog objekta x odredjuje na osnovu polozaja tog objekta u odnosu na sebe x' i polozaja sebe u odnosu na referentno telo xo=vt izmereno laserom i satom. Bez obzira da li on zna za Galilejeve transformacije ili ne on ih koristi x=x'+xo=x'+vt.



#!/usr/bin/basho
mv frog ancient_pond
echo "Splash!"
 
0

srki
Srdjan Mitrovic
Auckland, N.Z.

Član broj: 2237
Poruke: 3654
*.dialup.xtra.co.nz



+3 Profil

icon Re: Teorija Relativnosti25.07.2004. u 16:41 - pre 253 meseci
Citat:
Ne, posmatrac 2 koji "misli" da se krece koristi Galilejeve transformacije iz inercijalnog u neinercijalni koordinatni sistem t'=t x'=x-vt.

Ako se krece nepromenjivom brzinom u odnosu na drugi koordinatni sistem onda su ili oba sistema inercijalni ili su oba sistema neinercijalni.

Citat:
On misli da se krece brzinom v, dakle po njemu njegove prostorne koordinate (njegove trajektorije) xo se menjaju, odnosno izvoriste njegovog koordinatnog sistema je vezano za neki drugi (referentni) objekat za koji on misli da miruje, dok sat sa koga ocitava vreme t drzi u ruci. Polozaj nekog objekta x odredjuje na osnovu polozaja tog objekta u odnosu na sebe x' i polozaja sebe u odnosu na referentno telo xo=vt izmereno laserom i satom. Bez obzira da li on zna za Galilejeve transformacije ili ne on ih koristi x=x'+xo=x'+vt.


Ti sve vreme pricas o klasicnoj mehanici?
 
0

Cybernoid II

Član broj: 14852
Poruke: 528

Sajt: www.youtube.com/watch?v=7..


+1 Profil

icon Re: Teorija Relativnosti25.07.2004. u 16:52 - pre 253 meseci
Citat:
Ti sve vreme pricas o klasicnoj mehanici?


Ne, govorim o difeomorfizmu i invarijantama o odnosu na transformacije koordinata, iliti o opstoj teoriji relativnosti.

Citat:
Ako se krece nepromenjivom brzinom u odnosu na drugi koordinatni sistem onda su ili oba sistema inercijalni ili su oba sistema neinercijalni.


Izvini, sta je po tebi inercijalni koordinatni sistem?

http://www.meta-religion.com/P...more_practical_arrangement.htm
Citat:
An inertial coordinate system is a system of space and time coordinates with respect to which inertia is homogeneous and isotropic.
Odnosno talasna jednacina ima kanonicki oblik.
#!/usr/bin/basho
mv frog ancient_pond
echo "Splash!"
 
0

srki
Srdjan Mitrovic
Auckland, N.Z.

Član broj: 2237
Poruke: 3654
*.dialup.xtra.co.nz



+3 Profil

icon Re: Teorija Relativnosti25.07.2004. u 17:27 - pre 253 meseci
Pa ako se ja krecem konstantnom brzinom u odnosu na inercijalni sistem onda ce i moj sopsveni sistem isto biti inercijalni. A ti si pominjao transformaciju iz inercijalnog u neinercijalni.
 
0

Cybernoid II

Član broj: 14852
Poruke: 528

Sajt: www.youtube.com/watch?v=7..


+1 Profil

icon Re: Teorija Relativnosti25.07.2004. u 18:02 - pre 253 meseci
Citat:
Pa ako se ja krecem konstantnom brzinom u odnosu na inercijalni sistem onda ce i moj sopsveni sistem isto biti inercijalni.


Sta znaci izraz "moj sopstveni sistem"? Koordinatni sistem je proizvoljno jednoznacno mapiranje vektorskog prostora u R^4 koje svakom dogadjaju dodeljuje uredjenu 4-ku realnih brojeva.
#!/usr/bin/basho
mv frog ancient_pond
echo "Splash!"
 
0

Nedeljko
Nedeljko Stefanović

Nedeljko
Član broj: 314
Poruke: 8706
*.dial.InfoSky.Net



+2802 Profil

icon Re: Teorija Relativnosti25.07.2004. u 18:12 - pre 253 meseci
Citat:
Cybernoid II: sta koristi oci ili instrumente?


Izvinjavam se, ali ja sam do sada mislio da su i oči jedan (prirodni) merni instrument za merenje talasnih dužina svetlosti koja iz raznih tačaka dopire u njega, kao i da se taj merni instrument podvrgava istim prirodnim zakonima kao i ostali. Ako naše prirodne oči ne mogu da registruju zračenje iz dela spektra relevantnog za Mesbauerov eksperiment, možemo se pomoći veštačkim "očima" (tj. mernim insrumentima). I jedno i drugo meri objektivnu realnost sa na[e ta;ke gledišta.

Citat:
Cybernoid II: On misli da se krece brzinom v, dakle po njemu njegove prostorne koordinate (njegove trajektorije) xo se menjaju, odnosno izvoriste njegovog koordinatnog sistema je vezano za neki drugi (referentni) objekat za koji on misli da miruje, dok sat sa koga ocitava vreme t drzi u ruci. Polozaj nekog objekta x odredjuje na osnovu polozaja tog objekta u odnosu na sebe x' i polozaja sebe u odnosu na referentno telo xo=vt izmereno laserom i satom. Bez obzira da li on zna za Galilejeve transformacije ili ne on ih koristi x=x'+xo=x'+vt.


I ne radi se o tome šta on misli, već o tome kako će videti spoljni svet bez obzira da li je učio Fiziku ili ne. Kako može da koristi nešto što ne zna?
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
 
0

Cybernoid II

Član broj: 14852
Poruke: 528

Sajt: www.youtube.com/watch?v=7..


+1 Profil

icon Re: Teorija Relativnosti25.07.2004. u 18:26 - pre 253 meseci
Citat:
I ne radi se o tome šta on misli, već o tome kako će videti spoljni svet bez obzira da li je učio Fiziku ili ne


Ja sam mislio sa se radi o tome kako ce on kvantitativno opisati brojevima i jednacinama ono sto on vidi. To je posao fizike zar ne?

A u stvari sve vreme je poenta bila subjektivni osecaj toka vremena, da li ono tece brze ili sporije.

Onda bi ovu temu trebalo premestiti u MadZone.
#!/usr/bin/basho
mv frog ancient_pond
echo "Splash!"
 
0

Nedeljko
Nedeljko Stefanović

Nedeljko
Član broj: 314
Poruke: 8706
*.dial.InfoSky.Net



+2802 Profil

icon Re: Teorija Relativnosti25.07.2004. u 18:29 - pre 253 meseci
Vrlo dobro se zna šta znači izraz "referentni sistem posmatrača O". Inače, engleski izraz mapping se kod nas (kada je Matematika u pitanju) prevodi kao preslikavanje (odnosno funkcija).

Referentni sistem može biti preslikavanje sizičkog prostor-vremena (spolnog sveta) u realan četvorodimenzioni vektorski prostor. Vektori su upravo te četvorke o kojima govoriš i ne pripadaju domenu, već kodomenu. Dobro de, i u spoljnom svetu izborom orjentacije i jedinične duži možeš uvesti vektore i operacije nad tim vektorima, inače ne bismo mogli govoriti o vektorskim fizičkim veličinama.

Dakle, ti tada moraš preslikati i tog posmatrača koji je takođe deo fizičkog sveta, pa je njegov koordintni sistem zapravo onaj koordinatni sistem u kome se on uvek nalazi u koordinatnom početku i u kome se svetlost u vakuumu kreće po geodezijskim linijama.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
 
0

Cybernoid II

Član broj: 14852
Poruke: 528

Sajt: www.youtube.com/watch?v=7..


+1 Profil

icon Re: Teorija Relativnosti25.07.2004. u 19:03 - pre 253 meseci
Citat:
Dakle, ti tada moraš preslikati i tog posmatrača koji je takođe deo fizičkog sveta, pa je njegov koordintni sistem zapravo onaj koordinatni sistem u kome se on uvek nalazi u koordinatnom početku i u kome se svetlost u vakuumu kreće po geodezijskim linijama.


Svetlost se uvek krece po geodezijskim null linijama.
Ako posmatrac misli da se krece u u odnosu na svoj koordinatnom sistem onda on ne lezi na liniji duz koje su prostorne koordinate jednake nuli.

Citat:
Vrlo dobro se zna šta znači izraz "referentni sistem posmatrača O".

Znacenje se podrazumeva, ali kako glasi tacna definicija?
"Referentni sistem vezan za posmatrača O u odnosu na koga on miruje" je nesto drugo.
"Ortonormirani referentni sistem vezan posmatrača O u odnosu na koga on miruje" je nesto trece.
"Klasa ekvivalentnih referentnih sistema..." je nesto cetvrto.
#!/usr/bin/basho
mv frog ancient_pond
echo "Splash!"
 
0

Nedeljko
Nedeljko Stefanović

Nedeljko
Član broj: 314
Poruke: 8706
*.dial.InfoSky.Net



+2802 Profil

icon Re: Teorija Relativnosti25.07.2004. u 19:57 - pre 253 meseci
Svetlost se ne kreće uvek po geodezijskim linijama bez dodatnih pretpostavki o metrici. Metrika se zapravo BIRA tako da svetlost u vakuumu u istim vremenskim razmacima prelazi isti put, a u takvoj metrici su geodezijske linije upravo putanje fotona u vakuumu. To su koordinatni sistemi u kojima ova priča može da ima ikakvog smisla i u kojima kada okreneš štap ili ga pomeriš, taj štap ne menja dužinu.

Recimo, ti možeš da skaliraš prostor po nekoj od prostornih koordinata, pa u tom novom koordinatnom sistemu jedinični pomak u pravcu te ose neće predstavljati isti put kao duž drugih prostornih osa. U toj metrici kada okreneš štap, on menja svoju dužinu. Zbog toga ta metrika nije fizički relevantna, iako je matematički moguća.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
 
0

Cybernoid II

Član broj: 14852
Poruke: 528

Sajt: www.youtube.com/watch?v=7..


+1 Profil

icon Re: Teorija Relativnosti25.07.2004. u 20:33 - pre 253 meseci
Citat:
Svetlost se ne kreće uvek po geodezijskim linijama bez dodatnih pretpostavki o metrici. Metrika se zapravo BIRA tako da svetlost u vakuumu u istim vremenskim razmacima prelazi isti put
.

Metrika je intristicka osobina prostora koja definise invarijantna infinitezimalna rastojanja u bezdimenzionalnim velicinama, dok su koordinate i jedinice mere te koje se biraju.
Metricka forma ima razlicite oblike u razlicitim koordinatnim sistemima i reskaliranje u jednom pravcu je samo promena oblika metricke forme prelazom u novi koordinatni sistem koji duzine ostavlja invarijantnim.

#!/usr/bin/basho
mv frog ancient_pond
echo "Splash!"
 
0

Nedeljko
Nedeljko Stefanović

Nedeljko
Član broj: 314
Poruke: 8706
*.dial.InfoSky.Net



+2802 Profil

icon Re: Teorija Relativnosti26.07.2004. u 02:45 - pre 253 meseci
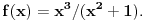
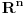
Ja ne znam kako ti shvataš prostor, ali na istom skupu tačaka se mogu zadati razne metrike. Recimo, neka je Nije teško pokazati da je to jedna rastuća nelinearna beskonačno-diferencijabilna bijakcija skupa realnih brojeva na samog sebe koja nulu preslikava u nulu u nulu. Uvedi umesto euklidske metrike u prostor sledeću metriku:

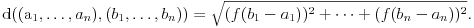
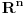
I to će biti metrika u prostoru jer će zadovoljiti sve aksiome metrike iz teorije metričkih prostora. No, nisam morao ići tako daleko. Mogao sam dati primer i sledeće metrike u

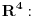
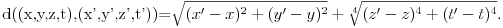
Međutim, iako su to metrike u matematičkom smislu potpuno ravnopravne sa svim ostalim, one nisu fizički relevantne. Dakle, ako bih u spoljnom svetu najpre izabrao pravougli dekartov koordinatni sistem, a potom rastojanje računao sa tim koordinatama po nestandardnim formulama (kao što su one gore), onda bih na istom skupu tačaka dobio sasvim drugačiju metriku sa sasvim drugim geodezijskim linijama.

Ako bih se tvrdoglavo držao takve metrike pri svim svojim merenjima, onda bi isti štap menjao svoju dužinu u toj metrici kada ga pomerim ili okrenem. I sa takvom metrikom bi se mogle dobiti iste fizičke teorije, samo što bi se jednačine promenile i strašno iskomplikovale. Od svih teorija koje podjednako dobro opisuju eksperimente najbolja je ona koja je najjednostavnija.

E zato fizičare ne interesuju takve metrike, iako su matematički potpuno ravnopravne sa svim drugim. Ono što si napisao o metrici se upravo svodi na to da štap ne menja dužinu kada ga zarotiramo ili transliramo. No, to je itekako izbor metrike. Sasvim je druga stvar što svi fizičari koriste istu metriku, to jest, što je taj izbor prećutan. Drugim rečima, izbor je jednom napravljen i dogovoren i niko ne koristi drugu metriku. Ta metrika je u potpunosti određena multiplikativnom konstantom, odnosno izborom merne jedinice.

Međutim, Matematika dopušta uvodjenje različitih metrika. Svaka funkcija koja zadovolji neke uslove se u Matematici zove metrikom, i za svaku takvu funkciju važe odgovarajuće matematičke teoreme. E, tu već dolazimo do jedne od razlika između Matematike i Fizike. U Fizici se koristi jedna jedina metrika, a u Matematici se mogu zadavati razne metrike.

Kada fizičar menja koordinatni sistem, on izračunava matematički oblik te metrike u drugom koordinatnom sistemu. To je zato što on metriku ne menja. On želi da izračuna u drugom koordinatnom sistemu dužinu štapa koji miruje u prvom koordinatnom sistemu. Drugim rečima, on izračunava iz različitih koordinatnih sistema isto rastojanje. Ali u Matematici je moguće razmatrati i različita "rastojanja".
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
 
0

-zombie-
Tomica Jovanovic
freelance programmer
ni.ac.yu

-zombie-
Član broj: 4128
Poruke: 3448
195.252.85.*

Sajt: localhost


+5 Profil

icon Re: Teorija Relativnosti26.07.2004. u 02:55 - pre 253 meseci
mnogo ste otišli u apstraktno, jedva vas pratim.. ;)

zato postavljam jedno prilično laičko, prizemno i konkretno pitanje (čini mi se slično onome što sprečo hoće da pita, samo uprošćeno):

situacija: klasičan "paradox" blizanaca, A ostaje na zemlji, B leti 20 godina tamo i 20 godina nazad, brzinom ~0.8c..

pitanje: kako se određuje kome će u stvari vreme brže proći, tj ko će na kraju biti stariji?

znači, kada loptu upute prema mojoj glavi, potpuno je ekvivalentno (sa stanovišta fizike, ne i "logike" ;), da kažemo da moja glava leti prema lopti (istom brzinom, istim pravcem, samo suprotnim smerom).

sve fizičke računice mogu da se izvedu u referentnom sistemu lopte, kao i u referentnom sistemu moje glave, i sve će pokazati potpuno ekvivalentni rezlutat (ako dovoljno brzo ne sklonim glavu, lopta će je pogoditi.. ;)

dakle, sa stanovišta "klasične" fizike, potpuno je nebitno da li moja glava juri na loptu, ili obrnuto..

kako se stvari menjaju pri relativističkim brzinama? i blizanac B isto može da kaže "blizanac A se od mene prvo udaljavao 20 godina, pa zatim približavao isto 20 godina".. zašto ne može?
blogče :: unescaped beta
　 » go-paste extenzija
　 » reč dana: backup
　 » bočne koalicije
 
0

elitemadzone.org :: MadZone :: Teorija Relativnosti
(Zaključana tema (lock), by Tyler Durden)
Strane: < .. 1 2 3 4 5 6 7 8 9 ... Dalje > >>

[ Pregleda: 475787 | Odgovora: 2583 ] > FB > Twit

Postavi temu

Srodne teme
Navigacija
Lista poslednjih: 16, 32, 64, 128 poruka.